3D Rotations
by Gabriel TaubinIEEE Computer Graphics and Applications Volume 31, Issue 6, pages 84 - 89, November-December 2011
3D Rotations are used everywhere in Computer Graphics, Computer Vision, Geometric Modeling and Processing, as well as in many other related areas. However, manipulating 3D Rotations is always confusing, and debugging code that involves 3D rotation is usually quite time consuming. There are many different, and apparently unrelated, ways of describing 3D rotations, such as orthogonal matrices, turns around vectors, quaternions, and the exponential map. Using elementary concepts from algebra, analytic geometry and calculus, in this article we reveal the relations existing amongst all these representations, and a few others which are not so well known. In summary, it is all about different, but closely related, parameterizations of the group of 3D rotations. The main goal is to produce simple, elegant, and efficient code, while paying close attention to the computational cost, and in particular trying to avoid computing transcendental functions and square roots.
Rotation Matrix
We start with the Algebraic Representation. A 3D rotation can be represented as an orthogonal \(3\times 3\) matrix \(Q\). That is, a matrix \(Q\) with its transpose equal to its inverse \(QQ^t=I\), where \(I\) is the identity matrix, and with unit determinant \(|Q|=1\). The result of applying a rotation to a 3D vector \(v\) is obtained by multiplying the matrix by the vector \(Q\,v\), an operation which requires 9 multiplications and 6 additions. The set of all such matrices form an algebraic group with respect to the operation of matrix multiplication called the special orthogonal group, and is denoted \(SO(3)\).
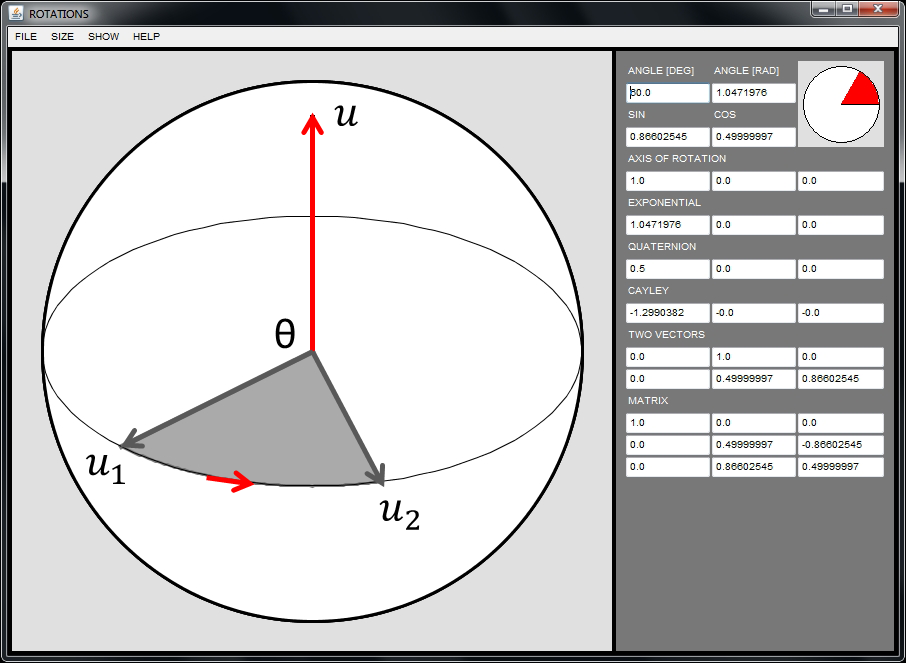
Rotation Around a Vector
We will also consider the Geometric Representation, which is a more intuitive way of describing a 3D rotation as a turn of angle \(\theta\) around a unit-length 3D vector \(u\), with the positive direction of rotation specified by the right hand rule. We denote such rotation \(Q(\theta,u)\).
Since the geometric representation has a more intuitive meaning, it is used whenever a 3D rotation has to be modified. For example to change the viewpoint within a 3D viewer or modeling system. However, when the same rotation has to be applied to a large number of vectors, the algebraic representation is easier to use, and most often less computationally expensive to evaluate.
The first question to ask is what is the relation between these two representations? Can we go back and forth between the two? More specifically, is it true or false that each rotation matrix \(Q\) can be described as a rotation of a certain angle \(\theta\) around a unit vector \(u\) or not? If so, how do we determine the vector and the angle? Also, is this description unique? Conversely, given a unit vector and an angle, what is the corresponding algebraic representation of the 3D rotation? We are going to answer all these questions and many more.
We can start by answering the question about uniqueness for the geometric representation: it is not. The rotation of an angle \(\theta\) around a unit vector \(u\) is indistinguishable from the rotation of an angle \(\theta+2k\pi\) around the same vector \(Q(\theta+2k\pi,u)=Q(\theta,u)\), and this is true for every integer \(k\). In particular, the rotation of angle \(2\pi\) (\(360^\circ\)) around any vector is identical to the identity. In other words, applying such rotation is equivalent to not doing anything. Also, the rotation of angle \(-\theta\) around the vector \(-u\) is identical to the rotation of angle \(\theta\) around \(u\). That is, \(Q(-\theta,-u)=Q(\theta,u)\).
Rodrigues' Formula
What about computing the algebraic representation of a 3D rotation from the geometric representation? The matrix representation of the rotation \(Q(\theta,u)\) is given by Rodrigues' formula \begin{equation} Q(\theta,u) = I+s\,U+(1-c)\,U^2 \label{rodrigues-formula} \end{equation} where \(I\) is the \(3\times 3\) identity matrix, \(s=\sin(\theta)\), \(c=\cos(\theta)\), and \(U\) is the skew-symmetric (\(U^t=-U\)) matrix \[ U=\left( \begin{matrix} 0 & -u_z & u_y \cr u_z & 0 & -u_x \cr -u_y & u_x & 0 \end{matrix} \right)\;. \] corresponding to the vector product by the vector \(u\). That is, for every 3D vector \(v\), we have \[ U\, v = u\times v = \left( \begin{matrix} u_y\,v_z - u_z\,v_y \cr u_z\,v_x - u_x\,v_z \cr u_x\,v_y - u_y\,v_x \end{matrix} \right)\;. \] We will leave to the reader to verify by direct computation that \(U^2=uu^t-I\).
Now, where does Rodrigues' Formula come from? We can explain it using plain and simple analytic geometry. Let \(Q=Q(\theta,u)\) be the algebraic representation of the 3D rotation that we are looking for, and let \(v\) be an arbitrary 3D vector. We want to find an expression for the 3D vector \(Qv\) as a function of \(\theta\), \(u\), and of course \(v\). We start by decomposing the 3D vector \(v\) into the sum of two orthogonal 3D vectors \[ v = (uu^t)\,v + (I-uu^t)\,v\;. \] The first one \(v_0=(uu^t)\,v=\lambda\,u\) is the orthogonal projection of \(v\) onto the line spanned by \(u\). This is the vector \(u\) scaled by the inner product \(\lambda=u^tv\) of \(u\) and \(v\). The second vector is the difference \(v_1=v-v_0\), which is a 3D vector orthogonal to \(u\), and so, also to \(v_0\). Since the multiplication by a matrix is a linear operation, we have \(Qv=Qv_0+Qv_1\), and the problem reduces to finding expressions for \(Qv_0\) and \(Qv_1\) as functions of \(\theta\), \(u\) and \(v\). Since the rotation is around the vector \(u\), and \(v_0\) and \(u\) are collinear, we have \(Qv_0=v_0\). For the other term, let \(v_2=u\times v_1=u\times v\). Since \(u\) is unit length, and \(u\) and \(v_1\) are orthogonal vectors, the two 3D vectors \(v_1\) and \(v_2\) are also orthogonal to each other and of the same length. In the plane spanned by \(v_1\) and \(v_2\), the rotation of angle \(\theta\) of vector \(v_1\) around the vertical direction \(u\) can be written as \[ Qv_1 = c\,v_1+s\,v_2\;, \] where \(s=\sin(\theta)\), and \(c=\cos(\theta)\) as before. If we combine all these expressions we obtain \[ Qv =Qv_0+Qv_1= (uu^t)\,v + c\,(I-uu^t)\,v + s\,u\times v\;. \] Finally, rearranging terms and remembering that \(U=uu^t-I\), we obtain the desired result \[ Qv = v + s\,u\times v + (1-c)\,(uu^t-I)\,v = (I+s\,U+(1-c)\,U^2)\,v\;. \]
So far we have shown that a 3D rotation specified by a unit vector \(u\) and angle \(\theta\) can be represented as a rotation matrix \(Q=Q(\theta,u)\), and we know that this mapping \((\theta,u)\mapsto Q(\theta,u)\) is not 1-1, since rotations around the same vector that differ in \(2\pi\) produce identical rotation matrices. But is it true or false that all rotation matrices \(Q\in SO(3)\) can be described as the rotation of a certain angle around a unit vector? If so, how can we determine suitable vector and angle?
The Exponential Map
To answer the last question we introduce the Exponential Map, which is defined by a power series \[ v\mapsto e^V = I + \sum_{n=1}^\infty \frac{1}{n!}\,V^n\;, \] where \(v\) is an arbitrary 3D vector \(v\), and \(V\) is the skew-symmetric matrix defined by \(v\) (\(V=\theta U\)). This formula is well defined because the power series on the right hand side converges absolutely to a finite square matrix, for every square matrix \(V\), not only for skew-symmetric matrices. We leave to the reader to verify that \(e^V\) is an orthogonal matrix when \(V\) is skew-symmetric.
Why have we introduced the Exponential Map? Because Rodrigues' formula turns out to be an efficient algorithm to evaluate the exponential map. In fact, we will show now that \(e^V=Q(\theta,u)\). for \(v=\theta u\) (the value of \(u\) is irrelevant if \(\theta=0\)). \[ e^V=e^{\theta U} = I + \sum_{n=1}^\infty \frac{\theta^n}{n!}\,U^n\;, \] From the identity \(U^3+U=0\), which can be verified by direct expansion, it follows that \(U^{2k+1}=(-1)^k U\) for \(k\geq 0\) and \(U^{2k} = -(-1)^kU^2\) for \(k\geq 1\). Splitting the previous series expansion into even and odd terms, replacing these identities, and rearranging terms, we obtain \[ e^{\theta U} = I + \left(\sum_{k=0}^\infty \frac{(-1)^k\theta^{2k+1}}{(2k+1)!}\right)\,U\; +\left(1- \sum_{k=0}^\infty \frac{(-1)^k\theta^{2k}}{(2k)!}\right)\,U^2\;. \] Finally, we observe that the two power series of the real number \(\theta\) in this last expression are nothing but the power series expansions of \(s=\sin(\theta)\) and \(c=\cos(\theta)\) respectively, which follows from Euler's Formula \(c+js=e^{j\theta}\). In fact, Euler's Formula can be regarded as the definition of the functions \(\cos(\theta)\) and \(\sin(\theta)\). Here \(e^{j\theta}\) is the exponential of a complex number, which is defined by the same power series expansion as the exponential of a real number, or the exponential of a square matrix shown above, and \(j\) is the square root of \(-1\) \[ e^{j\theta} = \sum_{n=0}^\infty \frac{(j\,\theta)^n}{n!} = \left(\sum_{k=0}^\infty \frac{(-1)^k\theta^{2k}}{(2k)!}\right)+ j\left(\sum_{k=0}^\infty \frac{(-1)^k\theta^{2k+1}}{(2k+1)!}\right) \] Readers exposed to signal processing concepts should be familiar with Euler's Formula.
The Logarithm Map
The exponential map with the whole Euclidean three-dimensional space as domain is onto, i.e., every rotation can be represented as an exponential of a skew symmetric matrix. However this map not one-to-one. We are not going to prove this fact here. We will leave this task to the reader as well. But we will show how to compute the inverse map. In order to do so, we first need to restrict the domain to a smaller open subset of \({\cal R}^3\) where the exponential map is one-to-one. To determine such subset, note that the map \(\theta\mapsto e^{\theta U}\) with fixed \(u\) is \(2\pi\)-periodic, and for \(\pi\leq\theta\leq 2\pi\) we have \[ e^{\theta U} = e^{(2\pi-\theta) (-U)}\;, \] i.e., the rotation of angle \(\theta\) around \(u\) is equal to the rotation of angle \(2\pi-\theta\) around \(-u\). When the domain is restricted to the open ball of radius \(\pi\) \[ \Omega_\pi =\{ v : \|v\|<\pi\} =\{ \theta u : 0\leq \theta<\pi\;,\;\|u\|=1\}, \] the exponential map becomes \(1-1\), but rotations of angle \(\pi\) cannot be represented. The image of \(\Omega_\pi\) through the exponential map, i.e., the set of rotations of angle less than \(\pi\) around an arbitrary unit length vector, is an open neighborhood of the identity in the Lie group of 3D rotations \(SO(3)\).
Note that the set of rotations of angle \(\pi\) around an arbitrary unit length vector \(u\) are those satisfying the algebraic equation \[ |Q+I|=0 \] because in such a case any vector \(u_1\) orthogonal to \(u\) satisfies the equation \(Qu_1=-u_1\), i.e., it is an eigenvalue of \(Q\) corresponding to the eigenvalue \(-1\).
On the set of rotations of angle less than \(\pi\) the exponential map has a well defined inverse: the Logarithm Map. The logarithm of a rotation \(Q\) of angle less than \(\pi\) can be computed by following these steps \begin{equation} \left\{ \begin{matrix} c & = & (1-\hbox{trace}\,(Q))/2 \cr V & = & (Q-Q^t)/2 \cr s & = & \|v\| \cr u & = & v / s \cr \theta & = & \hbox{angle}_{[0,\pi)}(s,c) \;. \cr \end{matrix} \right. \label{computing-the-logarithm} \end{equation}
Where do these step come from? Since the rotation matrix \(Q\) is in the range of the exponential map, it can be written as \(Q=Q(\theta,u)=I+sU+(1-c)U^2\). Since the transpose of \(Q\) is equal to the inverse of \(Q\), we have \(Q^t=Q^{-1}=Q(-\theta,u)=I-sU+(1-c)U^2\). Subtracting \(Q^t\) from \(Q\) we obtain the skew-symmetric matrix \(V=(Q-Q^t)/2=sU\). It follows that \(s=\|v\|\) must be equal to the norm the vector \(v\). This number could be equal to zero or not.
If \(s\) is not equal to zero, we can obtain the unit length vector \(u\) by normalizing \(v\) to unit length \(u=v/s\). But the angle of rotation is not yet uniquely determined since there are two angles, \(\theta\) and \(\pi-\theta\), between \(0\) and \(\pi\) for which the sine attains the same value. To uniquely identify the angle we need to determine whether the cosine of \(\theta\) is positive or negative. We can actually compute the cosine of \(\theta\) from the trace of \(Q\): \[ \begin{matrix} \hbox{trace}\,(Q) & = & \hbox{trace}(I)+s\,\hbox{trace}(U)+(1-c)\,\hbox{trace}(U^2)\cr & = & 3 + 0 + (1-c)(-2)\cr & = & 2c+1 \end{matrix} \] because \(\hbox{trace}\,(U^2)=\hbox{trace}\,(uu^t-I)= \|u\|^2-3 = -2\). It follows that \(c=(1-\hbox{trace}\,(Q))/2\).
On the other hand, if \(Q-Q^t=0\), or equivalently if \(s=0\), since \(s^2+c^2=1\), we have \(c=1\) or \(c=-1\). The \(c=1\) case corresponds to \(\theta=0\), the identity matrix \(Q=I\). The case \(c=-1\) corresponds to a rotation of angle \(\theta = \pi\). In this case the rotation matrix has the following form \[ Q=I+sU+(1-c)U^2= I+2(uu^t-I) = 2uu^t-I\;, \] and rearranging terms we obtain \[ \frac{1}{2}(Q+I) = uu^t = \left( \begin{matrix} u_x^2 & u_xu_y & u_xu_z \cr u_xu_y & u_y^2 & u_yu_z \cr u_xu_z & u_yu_z & u_z^2 \end{matrix} \right)\;. \] Since \(uu^t=(-u)(-u)^t\), it is clear now that if \(u\) is a solution to this problem, then so is \(-u\). Finally, the magnitudes of the components of the vector \(u\) can be obtained by computing the square roots of the diagonal elements of this matrix, and the signs from the off-diagonal elements: \[ \left\{\;\; \begin{matrix} u_x = \sqrt{(Q_{11}+1)/2}\cr \hbox{if} \; Q_{12}<0 \; \hbox{and} \; Q_{13}<0 \; \hbox{then}\cr \quad u_x=-u_x\cr u_y = \sqrt{(Q_{22}+1)/2}\cr \hbox{if} \; Q_{12}<0 \; \hbox{and} \; Q_{23}<0 \; \hbox{then}\cr \quad u_y=-u_y\cr u_z = \sqrt{(Q_{33}+1)/2}\cr \hbox{if} \; Q_{13}<0 \; \hbox{and} \; Q_{23}<0 \; \hbox{then}\cr \quad u_z = -u_z \end{matrix} \right. \]
Quaternions
Since in Rodrigues' Formula we have \(s^2+c^2=1\), let us consider the following mapping as a candidate to replace the exponential map \[ \left\{ \begin{matrix} \Omega_1 & \rightarrow & SO(3) \cr s u & \mapsto & I+s\,U+(1-c)\,U^2 \end{matrix} \right. \] where \(\Omega_1\) is the open unit ball in \({\cal R}^3\), \(0\leq s<1\), \(c=\sqrt{1-s^2}\), and \(|u|=1\). Rather than the angle of rotation itself, we use the sine of the angle as magnitude for the parameter vector \(v=su\). With this parametrization we are trying to avoid computing the sine and cosine of the angle \(\theta\). This parametrization is also \(1-1\), and only one square root is needed to evaluate it \begin{equation} \left\{ \begin{matrix} \Omega_1 & \rightarrow & SO(3) \cr v & \mapsto & I+\,V+\frac{1-\sqrt{1-\|v\|^2}}{\|v\|^2}\,V^2\;, \end{matrix} \right. \label{eq:v=su} \end{equation} where \(V=sU\) is the skew-symmetric matrix corresponding to the vector \(v=su\).
The only potential problem is that, since \(c\) is non-negative here, the image of \(\Omega_1\) through this parametrization is the set of rotations of angle less than \(\pi/2\), and so, not an onto map. To solve this problem we regard the magnitude \(s=\|v\|\) of a vector in \(\Omega_1\) not as \(\sin(\theta)\), but as \(\sin(\theta/2)\). Since \[ \left\{ \begin{matrix} 1-\cos(\theta) & = & 2\sin(\theta/2)^2 & = & 2s^2\cr \sin(\theta) & = & 2\sin(\theta/2)\cos(\theta/2) & = & 2sc\cr \end{matrix} \right. \] the following parametrization \begin{equation} \left\{ \begin{matrix} \Omega_1 & \rightarrow & SO(3) \cr s u & \mapsto & I+2sc\,U+2s^2\,U^2 \end{matrix}\right. \label{half-angle-parameterization} \end{equation} covers the same open set of rotations as the exponential map. Note that since in this case \(0\leq\,\sin(\theta/2)\,,\,\cos(\theta/2)\leq 1\), we can safely compute \(c\) as \(\sqrt{1-s^2}\), and by combining terms we can evaluate this parametrization also with a single square root: \begin{equation} \left\{ \begin{matrix} \Omega_1 & \rightarrow & SO(3) \cr v & \mapsto & I+2\,\sqrt{1-\|v\|^2}\,V+2\,V^2\;, \end{matrix} \right. \label{half-angle-parameterization-2} \end{equation} where \(V=sU\) is again the skew-symmetric matrix corresponding to the vector \(v=su\).
How do we compute the inverse of this parametrization? We will leave this as another exercise to the reader, but with two hints. First, it is easy to compute the norm of the parameter vector \(v\) from the trace of the matrix \(Q\). If this number is zero, then \(Q\) is the identity matrix. Otherwise, the vector \(v\) normalized to unit length can be computed from the skew-symmetric part \((Q-Q^t)/2\) of \(Q\).
It is interesting to observe now that this is the parametrization of the special orthogonal group associated with the Quaternions. Quaternions are particularly popular in Computer Graphics because only four parameters are needed to represent a rotation, as opposed to nine in matrix form, and composition of rotations corresponds to the product of quaternions (although the exponential map uses only three unconstrained parameters). A quaternion is a pair \((a,b)\), where \(a\in{\cal R}\) is a scalar, and \(b\in{\cal R}^3\) is a vector. The product of two quaternions \((a_1,b_1)\) and \((a_2,b_2)\) is defined by this formula \[ (a_1,b_1)\cdot(a_2,b_2) = (a_1 a_2-b_1^t b_2,a_1b_2+a_2b_1+b_1\times b_2)\;. \] If \(Q=Q(\theta,u)\) is the rotation of angle \(0\leq \theta <\pi\) around a unit-length vector \(u\), and \(v\) is an arbitrary 3D vector, the following identity is satisfied \begin{equation} (0,Qv) = (c,su)\cdot(0,v)\cdot(c,-su) \label{quaternion-parameterization} \end{equation} where \(c=\cos(\theta/2)\) and \(s=\sin(\theta/2)\), which the reader can verify this identity by direct computation.
Cayley's Rational Parametrization
If we also want to avoid computing square roots, we can use the following less known parametrization of the set of rotations of angle less than \(\pi\), due to Cayley \begin{equation} \left\{ \begin{matrix} {\cal R}^3 & \rightarrow & SO(3) \cr w & \mapsto & (I+W)^{-1}(I-W)=(I-W)(I+W)^{-1} \end{matrix}\right. \label{Cayley-parameterization} \end{equation} where \(W\) is the skew-symmetric matrix corresponding to the three-dimensional vector \(w\). Since \(|I-W|=|I+W|=1+\|v\|^2\), this function is well defined for any 3D vector \(w\). And surprisingly, the inverse of this parametrization is given by the same formula: if \(Q\) is a rotation of angle less than \(\pi\), then we have \(|I+Q|\neq 0\) and \(W=(I+Q)^{-1}(I-Q)\). To establish the relation with the other parameterizations, we observe that the expression \begin{equation} (I+W)^{-1} = I - \frac{1}{1+\|w\|^2}\,W + \frac{1}{1+\|w\|^2}\,W^2 \label{cayley-inverse} \end{equation} follows from the identity \(W^3+\|w\|^2 W=0\), and so \[ Q=(I+W)^{-1}(I-W) = I - \frac{2}{1+\|w\|^2}\,W + \frac{2}{1+\|w\|^2}\,W^2\;, \] which can be evaluated without square roots. If we now write \(w=-\mu u\) with \(\|u\|=1\) in the last equation, we obtain \begin{equation} Q = I + \frac{2\mu}{1+\mu^2}\,U + \frac{2\mu^2}{1+\mu^2}\, U^2\;, \label{cayley-parameterization-2} \end{equation} which es equal to the parametrization of equation \eqref{half-angle-parameterization} with \(\mu=\tan(\theta/2)\).
To apply one of these rotations to a vector \(v\) we can follow these steps \begin{equation} \left\{\;\; \begin{matrix} \mu & = & 2/(1+\|w\|^2)\cr v_1 & = & w\times v\cr v_2 & = & w\times v_1\cr Qv & = & v - \mu(v_1-v_2) \end{matrix} \right. \label{eq:apply-cayley} \end{equation} which require 19 multiplications and 14 additions. On the other hand, the \(3\times 3\) matrix \(Q\) can be constructed by following these steps \[ \left\{\;\; \begin{matrix} \mu & = & 2/(1+\|w\|^2)\cr Q & = & I-\mu \, W\cr Q & = & Q+\mu \, (ww^t-I) \end{matrix} \right. \] which require 22 multiplications and 14 additions. Since multiplying a \(3 \times 3\) matrix by a vector requires 9 multiplications and 6 additions, if the same rotation has to be applied to many vectors, the cost of constructing the matrix \(Q\) and then applying the rotation by matrix multiplication is about half compared to applying the steps described in equation \eqref{eq:apply-cayley} to each vector. However, if the rotation has to be applied to only one or two vectors before the parameter vector \(w\) changes, then applying the rotation by following the steps described in equation \eqref{eq:apply-cayley} is less expensive.
Rotation From 2 Unit Vectors
Another way of specifying a rotation is from two linearly independent unit length vectors \(u_1\) and \(u_2\), as a rotation \(Q=Q(u_1,u_2)\) that transform the vector \(u_1\) into \(u_2=Qu_1\). Since there is an infinite number of such rotations, we further require the rotation to minimize the turning angle amongst all such rotations. It turns out that with this additional constraint there is a unique solution. This is a rotation around the unit length vector \(u\) normal to the plane spanned by the two vectors, i.e., \(u_1\times u_2\) normalized to unit length, and the angle of rotation \(\theta\) is the one formed by the two vectors. The matrix \(Q=Q(\theta,u)\) can be computed using Rodrigues' formula without explicitly computing the angle of rotation, since the vector \(u\) and the sine and cosine of \(\theta\) can be determined directly from the two vectors: \begin{equation} \left\{ \begin{matrix} c & = & u_1^tu_2 \cr s & = & \sqrt{1-c^2} \cr u & = & u_1\times u_2 / s \end{matrix} \right. \label{from-2-vector-rodrigues} \end{equation} This can be extended with continuity to the case \(u_1=u_2\) by defining \(Q\) as the identity matrix, but it cannot be extended to the case \(u_1=-u_2\) because of lack of uniqueness: for every unit-length vector \(u\) orthogonal to \(u_1\), the rotation \(Q(\pi,u)\) transforms \(u_1\) into \(u_2\), and no rotation of angle less than \(\pi\) transforms \(u_1\) into \(u_2\).
But the matrix \(Q(u_1,u_2)\) can also be computed without evaluating square roots. Let \(v=u_1\times u_2\) and \(c=u_1^tu_2\). Since \(v=su\), we have \(I+V=I+sU\), and \[ (1-c)U^2=\frac{1-c}{s^2}V^2=\frac{1-c}{1-c^2}V^2=\frac{1}{1+c}V^2\;, \] and it follows that \[ Q(u_1,u_2)=I+V+\frac{1}{1+c^2}V^2\;. \] Note the relation between this formula and the one in equation \eqref{eq:v=su}. Here we avoid computing the square root because we can compute the cosine of the angle independently as an inner product.
Another way of computing \(Q(u_1,u_2)\) without square roots is using Cayley's rational parametrization. The reader can verify that when \(Q=(I+W)^{-1}(I-W)\), the vector \(w\) defining this rotation can be determined as follows: \begin{equation} \left\{ \begin{matrix} c & = & u_1^tu_2 \cr w & = &(u_1\times u_2)/(1-c) \end{matrix} \right. \label{from-2-vector-cayley} \end{equation}
Conclusion
In this article we have explored several popular and not so popular parameterizations of the group of 3D rotations, paying particular attention to the computational cost and algorithm development. We have seen that despite the apparent differences, all these parameterizations are closely related. And we did all of this with only a bit of algebra, analytic geometry and calculus. In a follow-up article we will explore applications of these methods, particularly to digital geometry processing problems.
