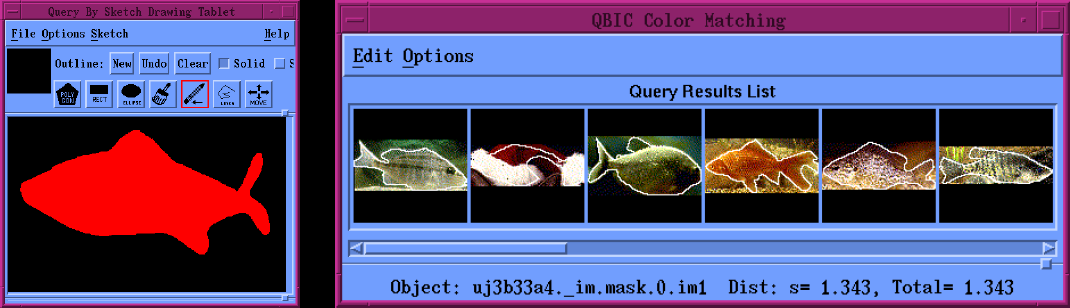
Image Database Search
Digital Geometry Processing (DGP)
3D Geometry Compression / 3D Broadcasting / Telepresence
Shape Capture / 3D Photography
3D Surface Reconstruction
3D Shape Capture for Heritage Preservation
Digital Archaeology / The REVEAL System
Dynamic Shape capture / 3D Cinematography
Interaction and Large Format Displays
Medical Imaging and Medical Devices
TOP
Image Database Search
Soon after I joined IBM, around 1991-1992, the Machine Vision group from the IBM Almaden Research Center started the Query By Image Content (QBIC) project. The goal of the project was to develop a system to query large on-line image databases using the images' content as the basis of the queries. Examples of features used to specify these queries include color, texture, and shape of image objects and regions. Today there is no need to justify such a project, but potential applications identified at the time included medical (`Give me other images that contain a tumor with a texture like this one'), photo-journalism (`Give me images that have blue at the top and red at the bottom'), and many others in art, fashion, cataloging, retailing, and industry. Key issues include derivation and computation of attributes of images and objects that provide useful query functionality, retrieval methods based on similarity as opposed to exact match, query by image example or user drawn image, the user interfaces, query refinement and navigation, high dimensional database indexing, and automatic and semi-automatic database population. In my Ph.D. thesis I introduced efficient algorithms to compute algebraic and moment invariants, and algorithms to fit algebraic curves and surfaces to data points, which I used to solve geometric matching and object recognition problems in Computer Vision. I contributed to the QBIC project by developing the shape feature extraction and matching algorithms based on this technology. Nowadays we are all familiar with web-based image search through services provided by companies such as Flickr, Google, Yahoo, Microsoft, and many others. But note that this project was well ahead of its time. It not only predates the creation of some of these companies and/or their image search services, but it also predates the introduction of Mosaic, the first web browser, which was released in January 1993. QBIC was the first image database search system to be released as a product, under the name Ultimedia Manager, during the summer of 1994. I applied the same technology in other projects. For example, I was responsible for the development and implementation of shape matching algorithms for the IBM VeggieVision produce recognition system. The system was successfully completed, and later commercialized as well.

- Ph.D. Electrical Engineering, Brown University, Providence, RI, May 1991. Thesis title: Recognition and Positioning of Rigid Objects using Algebraic and Moment Invariants.
- Object Recognition Based on Moment (or Algebraic) Invariants, by G. Taubin and D.B. Cooper. In Geometric Invariance in Computer Vision, J. Mundy and A. Zisserman, (eds.), MIT Press, 1992.
- 2D and 3D Object Recognition and Positioning with Algebraic Invariants and Covariants, by G. Taubin and D.B. Cooper. In Symbolic and Numerical Computation for Artificial Intelligence, B. Donald, D. Kapur, and J. Mundy, (eds.), Academic Press, 1992.
- The QBIC Project: Querying Images by Content Using Color, Texture, and Shape, by W. Niblack, R. Barber, W. Equitz, M. Flickner, E. Glasman, D. Petkovic, P. Yanker, and G. Taubin, Conference on Storage and Retrieval for Image and Video Databases, SPIE/SPSE Symposium on Electronic Imaging, February 1993, (Cited by 1826)
- VeggieVision: A Produce Recognition System, by R. Bolle, J. Connell, N. Haas, R. Mohan, and G. Taubin, Third IEEE Workshop on Applications of Computer Vision (WACV-96), Sarasota, Florida, December 1996.
TOP
Digital Geometry Processing (DGP)
My paper A Signal Processing Approach to Fair Surface Design helped to establish the mathematical foundations of DGP as a sub-field in Computer Graphics. In this paper I showed how to formulate Fourier analysis on polygonal meshes, and more generally on signals defined on graphs, generalizing the classical formulations for regularly sampled data. In the same paper I introduced a simple and efficient linear time and space smoothing algorithm to denoise the geometry of polygon meshes, and justified its behavior by showing that it implements a low-pass filter. This smoothing algorithm is now commonly associated with my name, and still cited by a large number of publications in the field. This work motivated a number of extensions and improvements by many researchers, including myself. For example, in Optimal Surface Smoothing as Filter Design I introduced an efficient algorithm to evaluate any filter with polynomial transfer function (FIR filters) expressed in the Chebyshev basis, and showed that all the classical methods to design FIR filters can be used without any change to design filters for signals defined on the vertices of graphs, and in particular of polygon meshes. These are not only low-pass filters, but arbitrary filters. The curvature of smooth surfaces plays the role of frequency of signals defined in Cartesian space (such as 1D sound and 2D images). In Estimating the Tensor of Curvature of a Surface from a Polyhedral Approximation I introduced an efficient algorithm to estimate the directional curvatures at any vertex of a polygonal mesh regarded as a discretization of a smooth surface. This paper is still widely cited as well. I am currently working on a variety of problems associated with the mathematical foundations of digital geometry processing, such as formulating and proving resampling theorems for polygonal meshes. These theorems would establish conditions under which the resolution of a polygonal mesh could be changed (uniformly or adaptively) without losing geometric information. I expect this work to have a significant impact in surface simplification and hierarchical surface representations such as subdivision surfaces. Algorithms for changing the sampling rate of a signal in the digital domain are taught in every digital signal processing course. A solution of such problem for irregular meshes would result in optimal mesh decimation algorithms. For example, in Dual Mesh Resampling I propose a simple algorithm to resample a manifold mesh according to the connectivity of its dual mesh. Simultaneous interpolating vertex position and normal constraints are difficult to impose on mesh denoising (smoothing) algorithms. Tangential drift is a related problem observed in meshes with irregular edge length and angle distribution. In Linear Anisotropic Mesh Filters I propose a simple solution to the problem as an extension of Laplacian smoothing. Within the context of the NSF grant titled Fundamental Geometry Processing I am continuing my exploration of problems in this domain, in particular as they relate to dynamic shapes, deformations, and interactive shape design. My work on surface reconstruction methods, described elsewhere in this report, can also be considered part of DGP, since surface smoothing (or regularization) is an integral component of most surface reconstruction algorithms.
- A Signal Processing Approach to Fair Surface Design, by G. Taubin, Siggraph'95, (Cited by 1164)
- Estimating the Tensor of Curvature of a Surface from a Polyhedral Approximation, by G. Taubin, Fifth International Conference on Computer Vision (ICCV'95), (Cited by 407)
- Curve and Surface Smoothing Without Shrinkage, by G. Taubin, Fifth International Conference on Computer Vision (ICCV'95), (Cited by 151)
- US Patent 05506947, Curve And Surface Smoothing Without Shrinkage, 04/09/1996
- Optimal Surface Smoothing as Filter Design, by G. Taubin, T. Zhang, and G. Golub, Fourth European Conference on Computer Vision (ECCV'96), (Cited by 108)
- Converting Sets of Polygons to Manifold Surfaces by Cutting and Stitching, by A. Gueziec, G. Taubin, F. Lazarus, and W. Horn, IEEE Visualization'98, 1998. Also presented as a Technical Sketch, Siggraph'98, Orlando, FL, July 1998, (Cited by 77)
- A Framework for Memory-Efficient Levels of Detail, by A. Gueziec, and G. Taubin, Tenth Canadian Conference on Computational Geometry, Montreal, Canada, August 1998.
- Geometric Signal Processing on Polygonal Meshes, Eurographics State of the Art Report, August 2000, (Cited by 146)
- 3D Mesh Geometry Filtering Algorithms for Progressive Transmission Schemes, by R. Balan and G. Taubin, Computer-Aided Design 32 (2000) 825-846, Special Issue on Multi-Resolution Geometric Models.
- US Patent 06016153, Method To Convert Non-Manifold Polyhedral Surfaces Into Manifold Surfaces, 01/18/2000
- Cutting and Stitching: Converting Sets of Polygons to Manifold Surfaces, by A. Gueziec, G. Taubin, F. Lazarus, and W. Horn, IEEE Transactions on Visualization and Computer Graphics, Vol. 7, No. 2, April-June 2001, pp. 136-151.
- Is This A Quadrisected Mesh?, by G. Taubin, Sixth ACM Symposium on Solid Modeling and Applications, Solid Modeling 2001, Ann Arbor, Michigan, June 2001.
- Dual Mesh Resampling, by G. Taubin, in Proceedings of Pacific Graphics 2001, Tokyo, Japan, October 2001.
- Linear Anisotropic Mesh Filters, by G. Taubin, IBM Research Technical Report RC-22213, October 2001
- US Patent 06307551, Method For Generating And Applying Changes In The Level Of Detail Of A Polygonal Surface, 10/23/2001
- Dual Mesh Resampling, by G. Taubin, Graphical Models, vol. 64, no. 2, pp. 94-113, 2002.
- Detecting and Reconstructing Subdivision Connectivity by G. Taubin, The Visual Computer, Special Issue on Subdivision, edited by A. Nasri, July 2002.
- Constructing Hamiltonian Triangle Strips on Quadrilateral Meshes, by G. Taubin, International Workshop on Visualization and Mathematics 2002, Berlin-Dahlem, Germany, May 2002.
- Image-Based Object Editing, by H. Rushmeier, J. Gomes, L. Balmelli, F. Bernardini, and G. Taubin, 4th International Conference on 3D Digital Imaging and Modeling, 3DIM 2003, October 2003.
- Constructing Hamiltonian Triangle Strips on Quadrilateral Meshes, in Visualizations and Mathematics III, Hans-Christian Hege and Konrad Polthier (eds.), Springer Verlag, 2003.
- Towards Real-Time Massive Geometry Signal Processing, by G. Taubin, BIRS Workshop on Mathematical Foundations of Scientific Visualization, Computer Graphics, and Massive Data Exploration, Banff International Research Station, Canada, May 2004.
- Atlas Aware Laplacian Smoothing, by P. G. Sibley and G. Taubin, IEEE Visualization 2004, Poster Session, October 2004.
- New Results in Signal Processing and Compression of Polygon Meshes, in Geometric Modeling for Scientific Visualization, Guido Brunnett, Bernd Hamann, and Heinrich Mueller (eds.), Springer Verlag 2004.
- US Patent 6943790, Dual Mesh Resampling, 09/13/2005.
- US Patent 6987511, Linear Anisotropic Mesh Filtering, 01/17/2006
- US Patent 07167173, Method And Structure For Image-Based Object Editing, 01/23/2007.
- US Patent 07174050, Space-Optimized Texture Maps, 02/06/2007.
- NSF Grant Title: “AF:Small:Fundamental Geometry Processing.” Started in September 2009. Currently active.
- Surface Deformations Driven by Vector-Valued 1-Forms, by G. Taubin, and C. Demiralp, IEEE International Conference on Shape Modeling and Applications (SMI) 2010.
- Surface Covering Curves, by Q. Xing, E. Akleman, G. Taubin and J. Chen, Symposium on Computational Aesthetics 2011, Vancouver, BC, Canada, August 2011
TOP
3D Geometry Compression / 3D Broadcasting / Telepresence

I was the main contributor to the development and implementation of 3D Geometry Compression technology at IBM Research. For a period of about four years I participated in the MPEG-4 standardization effort, leading the IBM team. In 1996 I helped draft the call for proposals. From 1997 to 2000, I served as co-editor of the 3D Mesh Coding specification, and co-developer of the corresponding reference software, which is normative part of the of the ISO/IEC 14496 (MPEG-4) international standard. This technology was also at the core of an earlier VRML Compressed Binary Format Proposal (1997), which later evolved into the technology incorporated into the MPEG-4 standard. Within IBM I was also the main contributor in the process of transferring the technology to the award-wining (PC Expo'2000 Best of Show Software) IBM HotMedia product. This was the first commercial product incorporating this technology. I served as project leader and co-developer of the authoring tools and Java-based players to visualize and interact with 3D models represented as colored or textured polygonal meshes. My paper Geometry Compression through Topological Surgery, published in 1998, was the first method proposed (in January 1996) to represent a manifold polygonal model in compressed form with no loss of connectivity information, and controllable loss of geometry and properties information. This paper, jointly with its sequels Progressive Forest Split and Efficient Compression of Non-Manifold Polygonal Meshes, constitute the core of the MPEG-4 3D Mesh Coding technology, and resulted in about ten (10) US patents. Polygon meshes are composed of connectivity and geometry. The connectivity describes how the vertices are interconnected forming polygon faces. The geometry describes the vertex positions in 3D as well as surface properties such as surface normal vectors, colors, and texture coordinates. Algorithms that operate on the connectivity of a mesh are combinatorial in nature, and I have made a number of additional contributions in the area as well. Most 3D geometry compression algorithms, as well as polygon mesh decimation algorithms, operate on both connectivity and geometry.

Within the context of the HP Labs Innovation Research grant titled Real-time View Morphing and 3D Video for Remote Collaboration and Tele-presence, and other pending NSF proposals, I am starting work on 3D broadcasting methods to compress, encode, and transmit dynamic 3D shapes captured by multi-view camera systems. I am developing data structures and algorithms to efficiently represent, compress, transmit, and remotely visualize dynamic 3D scenes, captured from multiple viewpoints, and visualized from multiple viewpoints. The work described elsewhere in this report on synchronized multi-view capture, modeling, and analysis of bat flight can be considered preliminary work in this direction as well.
- VRML'97 Course on The VRML Compressed Binary Format, G. Taubin, W.P. Horn and F. Lazarus (organizers and speakers), VRML'97, Monterey, CA, February 1997.
- Geometric Compression through Topological Surgery, by G. Taubin and J. Rossignac, ACM Transactions on Graphics, Vol. 17, No. 2, 1998.
- Surface Partitions for Progressive Loading and Display and Dynamic Simplification of Polygonal Surfaces, by A. Gueziec, F. Lazarus, and G. Taubin, VRML'98, Monterrey, CA, February 1998.
- Converting Sets of Polygons to Manifold Surfaces by Cutting and Stitching, by A. Gueziec, G. Taubin, F. Lazarus, and W. Horn, IEEE Visualization'98, 1998. Also presented as a Technical Sketch, Siggraph'98, Orlando, FL, July 1998.
- Siggraph'98 Course on 3D Geometry Compression, G. Taubin and J. Rossignac (organizers) Siggraph'98, Orlando, FL, July 1998.
- A Framework for Memory-Efficient Levels of Detail, by A. Gueziec, and G. Taubin, Tenth Canadian Conference on Computational Geometry, Montreal, Canada, August 1998.
- Progressive Forest Split Compression, by G. Taubin, A. Gueziec, W. Horn, and F. Lazarus, Siggraph'98, Orlando, FL, July 1998.
- Geometric Coding and VRML, by G. Taubin, W.P. Horn, F. Lazarus, and J. Rossignac, Proceedings of the IEEE, Special issue on multimedia signal processing, 1998.
- US Patent 05825369, Compression Of Simple Geometric Models Using Spanning Trees, 10/20/1998
- A Framework for Streaming Geometry in VRML, by A. Gueziec, G. Taubin, F. Lazarus, and B. Horn, IEEE Computer Graphics & Applications, special issue on VRML, Vol. 19, No. 2, March/April 1999.
- Efficient Compression of Non-Manifold Polygonal Meshes, by A. Gueziec, F. Bossen, G. Taubin, and C. Silva, IEEE Visualization'99, 1999.
- Siggraph'99 Course on 3D Geometry Compression, G. Taubin and J. Rossignac (organizers) Siggraph'99, Los Angeles, CA, August 1999.
- 3D Geometry Compression and Progressive Transmission, by G. Taubin, Eurographics State of the Art Report, September 1999.
- Multi-resolution Modeling and 3D Geometry Compression, by A. Gueziec, and G. Taubin, Computational Geometry: Theory and Applications, special issue on 3D Model Coding, Editing, and Transmission, Vol. 14, Issue 1-3, 30 November 1999, pp. 1-3.
- Efficient Compression of Non-Manifold Polygonal Meshes, by A. Gueziec, F. Bossen, G. Taubin, and C. Silva, Computational Geometry: Theory and Applications, special issue on 3D Model Coding, Editing, and Transmission, Vol. 14, Issue 1-3, 30 November 1999, pp. 137-166.
- US Patent 05905507, Compression Of Geometric Models Using Spanning Trees, 05/18/1999
- US Patent 06009435, Progressive Compression Of Clustered Multi-Resolution Polygonal Models, 12/28/1999
- US Patent 06031548 Progressive Multi-Level Transmission And Display Of Triangular Meshes, 02/29/2000
- 3D Mesh Geometry Filtering Algorithms for Progressive Transmission Schemes, by R. Balan and G. Taubin, Computer-Aided Design 32 (2000) 825-846, Special Issue on Multi-Resolution Geometric Models.
- US Patent 06184897, Compressed Representation Of Changing Meshes And Method To Decompress, 02/06/2001
- Cutting and Stitching: Converting Sets of Polygons to Manifold Surfaces, by A. Gueziec, G. Taubin, F. Lazarus, and W. Horn, IEEE Transactions on Visualization and Computer Graphics, Vol. 7, No. 2, April-June 2001, pp. 136-151.
- Is This A Quadrisected Mesh?, by G. Taubin, Sixth ACM Symposium on Solid Modeling and Applications, Solid Modeling 2001, Ann Arbor, Michigan, June 2001.
- ACM Solid Modeling '2001 Course on 3D Geometry Compression, organizer and speaker, Ann Arbor, Michigan, June 2001.
- Constructing Hamiltonian Triangle Strips on Quadrilateral Meshes, by G. Taubin, International Workshop on Visualization and Mathematics 2002, Berlin-Dahlem, Germany, May 2002.
- Detecting and Reconstructing Subdivision Connectivity by G. Taubin, The Visual Computer, Special Issue on Subdivision, edited by A. Nasri, July 2002.
- BLIC: Bi-Level Isosurface Compression, by G. Taubin, Proceedings of IEEE Visualization 2002, Boston, October 2002.
- Volume Warping for Adaptive Isosurface Extraction, by L. Balmelli, C. Morris, G. Taubin, and F. Bernardini, Proceedings of IEEE Visualization 2002, Boston, October 2002.
- Space-Optimized Texture maps, by L. Balmelli, G. Taubin, and F. Bernardini, in Proceedings of Eurographics 2002, Germany, October 2002 (Günter Enderle Best Paper Award).
- US Patent 06445389, Compression Of Polygonal Models With Low Latency Decompression, 09/03/2002
- US Patent 06452596, Method And Apparatus For The Efficient Compression Of Non-Manifold Polygonal Meshes, 09/17/2002
- US Patent 06307551, Method For Generating And Applying Changes In The Level Of Detail Of A Polygonal Surface, 10/23/2001
- New Results in Signal Processing and Compression of Polygon Meshes, in Geometric Modeling for Scientific Visualization, Guido Brunnett, Bernd Hamann, and Heinrich Mueller (eds.), Springer Verlag 2004.
- US Patent 07174050, Space-Optimized Texture Maps, 02/06/2007.
- US Patent 07230616, Bi-Level Isosurface Compression, 06/12/2007.
- US Patent 07847799 Bi-Level Isosurface Compression, 12/07/2010
- HP Labs Innovation Research Program grant, “Real-time View Morphing and 3D Video for Remote Collaboration and Tele-presence,” G. Taubin (PI). Started October 2011.
TOP
Shape Capture / 3D Photography

3D Photography stands for techniques and systems using cameras and lights to capture the shape and appearance of 3D objects. During my sabbatical at CalTech I started to work on the development of cost-effective 3D photography systems, and non-standard smart applications using consumer electronics devices (gadgets), such as PDAs, digital cameras, MP3 players, and cell-phones, which have powerful microprocessors, memory, sensors, display, and communication capabilities, and can be reprogrammed to perform tasks other than those they have been designed for. I taught a special projects course (named The Gadgets Lab) where students proposed and developed prototype implementations. I also taught at CalTech my 3D Photography class for the first time. Since I joined Brown I have taught this class at Brown on a regular basis, as well as at Siggraph in a full day format with the title Build Your Own 3D Scanner: 3D Photography for Beginners. The web site that we developed to support these courses receives a large number of visitors on a regular basis. I am currently working on converting the material developed for this courses into a textbook. Several final projects developed at the Brown version of the course evolved into conference and journal papers. In the paper Beyond Silhouettes: Surface Reconstruction using Multi-Flash Photography we exploit the computation of depth discontinuities from multi-flash image data to estimate the shape of an object from multiple images. In contrast to existing differential and global shape-from-silhouette algorithms, this method can reconstruct the position and orientation of points located deep inside concavities. Even though this technique produces more accurate shapes than those obtained with shape-from-silhouette techniques, points which do not produce an observable depth discontinuity because of visibility constraints cannot be reconstructed. When depth discontinuities are estimated as the object moves at constant speed along a continuous path in front of the camera, the method produces an unevenly sampled oriented point cloud. The surface reconstruction methods described elsewhere in this report were used to fill the resulting sampling gaps, resulting in a surface represented as a watertight polygon mesh. Extensions of this work were supported by NSF Grant titled Computing Shape From Depth Discontinuities. I have developed several other 3D Photography techniques, and plan to continue exploring this space in the near future.

- Applying Shape from Lighting Variation to Bump Map Capture, by H. Rushmeier, G. Taubin, and A. Gueziec, Eigth Eurographics Rendering Workshop, June 1997.
- Course on 3D Photography, 1st Symposium on 3D Data Processing, Visualization, and Transmission, speaker, Padova, Italy, June 2002.
- US Patent 06455835, System, Method, And Program Product For Acquiring Object Silhouettes For Shape Recovery, 09/24/2002
- US Patent 05974168, Acquiring Bump Maps From Curved Objects, 10/26/1999
- Beyond Silhouettes: Surface Reconstruction using Multi-Flash Photography, by Daniel Crispell, Douglas Lanman, Peter G. Sibley, Yong Zhao and Gabriel Taubin, Third International Symposium on 3D Data Processing, Visualization and Transmission, 3DPVT 2006, University of North Carolina, Chapel Hill, USA, June 2006.
- Surround Structured Lighting for Full Object Scanning, by D. Lanman, D. Crispell, and G. Taubin, Sixth International Conference on 3-D Digital Imaging and Modeling, 2007. 3DIM '07.
- Interactive 3D Scanning Without Tracking, L. Matthew, A. Vandergon, and G. Taubin, 20th. Brazilian Symposium on Computer Graphics and Image Processing (Sibgrapi 2007), Belo Horizonte, MG, Brazil, September 2007.
- NSF Grant Title: “Computing Shape From Depth Discontinuities,” G. Taubin (PI), September 2007-August 2010.
- US Patent (pending) Method And Apparatus For Surface Reconstruction Using Multi-Flash Photography, by D. Crispell, D. Lanman, P. G. Sibley, Y. Zhao, and G. Taubin, filed June 2008.
- 3D Slit Scanning with Planar Constraints, by M. Leotta, A. Vandergon, and G. Taubin, Computer Graphics Forum, Volume 27, Number 8, pp. 2066-2080, December 2008.
- Shield Fields: Modeling and Capturing 3D Occluders, by D. Lanman, R. Raskar, A. Agrawal, and G. Taubin, ACM Transactions on Graphics (TOG), Vol 27, Issue 5, December 2008, Siggraph Asia Proceedings.
- Siggraph 2009 Course: Build Your Own 3D Scanner: 3D Photography for Beginners, by D. Lanman, and G. Taubin, New Orleans, Los Angeles, August 2009 [http://mesh.brown.edu/byo3d]
- US Patent (pending), Surround Structured Lighting For Recovering 3d Object Shape And Apparance, by D. Crispell, D. Lanman, G. Taubin, filed August 2009.
- Shape From Depth Discontinuities under Orthographic Projection, by D. Lanman, D. Cabrini Hauagge, and G. Taubin, IEEE International Workshop on 3-D Digital Imaging and Modeling (3DIM'09), October 3-4, 2009, Kyoto, Japan
- One Shot Scanning Using DeBrujin Spaced Grids, by A. Osman Ulusoy, F. Calakli, and G. Taubin, IEEE International Workshop on 3-D Digital Imaging and Modeling (3DIM'09), October 3-4, 2009, Kyoto, Japan
- Surround Structured Lighting: 3-D Scanning with Orthographic Illumination, by Douglas Lanman, Daniel Crispell and Gabriel Taubin, Computer Vision and Image Understanding (CVIU), Volume 113, Issue 11, November 2009, Pages 1107-1117, Special issue on New Advances in 3D Imaging and Modeling.
- Siggraph Asia 2009 Course: Build Your Own 3D Scanner: 3D Photography for Beginners, by D. Lanman, and G. Taubin, Yokohama, Japan, December 2009
- Google Faculty Research Award Program, title: “3D Photography and Geometry Processing in Android,” G. Taubin (PI). Submitted August 2011 (under review).
TOP
3D Surface Reconstruction
3D Photography systems measure the shape of 3D objects from image, usually producing sets of 3D points as output. Sometimes additional properties are also measured, such as surface normal vectors or colors. Oriented point clouds are routinely obtained today from laser scanners, structured lighting systems, multi-view stereo algorithms, as well as from our 3D photography systems. 3D surface reconstruction techniques interpolate or approximate these points, producing surfaces as output, usually represented as polygon meshes. This problem has received an immense amount of attention in the literature, and I have been making contributions to this field since the mid 80’s. The algebraic curve and surface fitting algorithms that I introduced in Estimation Of Planar Curves, Surfaces And Nonplanar Space Curves Defined By Implicit Equations, With Applications To Edge And Range Image Segmentation, and in An Improved Algorithm for Algebraic Curve and Surface Fitting, were based on efficient approximations of the distance from a point to the zeros of a polynomial, and linear or non-linear least-squares algorithms. Extending these ideas, in Distance approximations for Rasterizing Implicit Curves and An Accurate Algorithm for Rasterizing Algebraic Curves and Surfaces I introduced efficient recursive subdivision algorithms to rasterize algebraic curves and surfaces guaranteed not to miss singularities.

More recently, in Vectorfield Isosurface-Based Reconstruction From Oriented Points and SSD: Smooth Signed Distance Surface Reconstruction, I introduced variational formulations to reconstruct a watertight surface defined by an implicit equation from a finite set of oriented points. I have shown that this approach constitutes an interesting alternative to other popular methods, it is much simpler to implement, and performs particularly well on unevenly sampled data sets at comparable cost. I am currently working on extending this method to handle dynamic point clouds, as well as silhouettes and sparse depth discontinuities estimated from optical flow and other methods. The problem of reconstructing colored 3D models from multiple images captured by inexpensive consumer level digital cameras has a wide range of applications in industry, entertainment, human-computer interaction, surveillance, navigation, archaeology, forensics, medicine, sports, architecture, and many other fields. Popular multi-view stereo algorithms produce dense colored oriented point clouds from collections of images.

Originally targeting the needs of our NSF Digital Archaeology project, we have recently extended our SSD Surface Reconstruction method to produce colored surfaces. The implicit surface color, which is extrapolated from the point colors, is represented as a scalar field defined on the bounding volume.

We are also exploring applications to view interpolation for face-to-face teleconferencing (in collaboration with HP Labs) which uses multiple synchronized video cameras, and the reconstruction will be performed in real time at video frame rate. In Accurate 3D Footwear Impression Recovery from Photographs we applied these techniques to forensic 3D reconstruction of footprints, and showed that this method is competitive with laser scanners.

- Nonplanar Curve And Surface Estimation In 3-Space, by G. Taubin. Proceedings, IEEE Conference on Robotics and Automation (R&A'88), Philadelphia, Pennsylvania, 1988.
- Estimation Of Planar Curves, Surfaces And Nonplanar Space Curves Defined By Implicit Equations, With Applications To Edge And Range Image Segmentation, by G. Taubin. In IEEE Transactions on Pattern Analysis and Machine Intelligence, November 1991.
- Constrained Implicit Function Fitting, by G. Taubin, B. Vemuri, and R.M. Bolle. 11th. International Conference on Pattern Recognition (ICPR'92), The Hague, Holland, September 1992.
- Parameterizing and Fitting Bounded Algebraic Curves and Surfaces, by G. Taubin, F. Cukierman, S. Sullivan, J. Ponce, and D.J. Kriegman. IEEE Conference on Computer Vision and Pattern Recognition (CVPR'92), Champaign, IL, June 1992.
- An Accurate Algorithm for Rasterizing Algebraic Curves, by G. Taubin. Second ACM/IEEE Symposium on Solid Modeling and Applications, Montreal, Canada, May 1993.
- An Improved Algorithm for Algebraic Curve and Surface Fitting, by G. Taubin. Fourth International Conference on Computer Vision (ICCV'93), Berlin, Germany, May 1993.
- Parameterized Families of Polynomials for Bounded Algebraic Curve And Surface Fitting, by G. Taubin, F. Cukierman, S. Sullivan, J. Ponce, and D.J. Kriegman. IEEE Transactions on Pattern Analysis and Machine Intelligence, March 1994.
- Implicit Simplicial Models I: Adaptive Curve Reconstruction, by G. Taubin and R. Ronfard, IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 18, No. 3, March 1996.
- The Ball-Pivoting Algorithm for Surface Reconstruction, by F. Bernardini, J. Mittleman, H. Rushmeier, C. Silva, and G. Taubin, IEEE Transactions on Visualization and Computer Graphics, Vol. 5, No. 4, October/December 1999, pp. 349-359.
- Estimating the in/out function of a surface represented by points, by V. Mello, L. Velho, G. Taubin, Proceedings of the 8th ACM Symposium on Solid Modeling and Applications, Seattle, WA, June 2003.
- Vectorfield Isosurface-Based Reconstruction From Oriented Points, by P. G. Sibley and G. Taubin, Siggraph 2005, Sketches Session, August 2005.
- Hierarchical G1 Smooth Surface Interpolation With Local Control, by G. Taubin, and W. Klug, Siggraph 2005, Poster Session, August 2005.
- Beyond Silhouettes: Surface Reconstruction using Multi-Flash Photography, by Daniel Crispell, Douglas Lanman, Peter G. Sibley, Yong Zhao and Gabriel Taubin, Third International Symposium on 3D Data Processing, Visualization and Transmission, 3DPVT 2006, University of North Carolina, Chapel Hill, USA, June 2006.
- Extracting Boolean Isosurfaces From Tetrahedral Meshes, by G. Taubin and P. Sibley, Siggraph 2006, Sketches Session, August 2006.
- NSF IIS program. Title: “III-CXT-Core Computer Vision Research: Promoting Paradigm Shifts in Archaeology” with D.B. Cooper, B.Kimia, and K. Galor. Submitted November 2007. Requested $2,638,964 for four year. Granted $2,638,964, starting in September 2008. Active.
- SSD: Smooth Signed Distance Surface Reconstruction, by F. Calakli, and G. Taubin, Pacific Graphics 2011, September 2011.
- SSD: Smooth Signed Distance Surface Reconstruction, by F. Calakli, and G. Taubin, Computer Graphics Forum, vol. 30, no. 7, 2011.
- Smooth Signed Distance Surface Reconstruction, by G. Taubin, Trimester Program on Computational Manifolds and Applications, Instituto Nacional de Matemática Pura e Aplicada (IMPA), Rio de Janeiro, Brazil, October 2011 (invited speaker).
- Accurate 3D Footwear Impression Recovery from Photographs, by F. A. Andalo, F. Calakli, G. Taubin, and S. Goldenstein, Proceedings of the 4th. International Conference on Imaging for Crime Detection and Prevention (ICDP-2011), Kington Upon Thames, London, UK, November 2011. Received Best Poster Award.
- An End-to-End Framework for Evaluation of Surface Reconstruction, by M. Berger, J. Levine, L. Nonato, C. Silva, and G.Taubin, ACM Transactions on Graphics (to appear).
TOP
3D Shape Capture for Heritage Preservation

As manager of the Visual and Geometric Computing Group at IBM Research I lead the Pieta project, where Michelangelo’s Florentine Pieta was 3D scanned and a 3D model comprising not only geometry but also texture and color information was reconstructed to support art historian Jack Wasserman in his comprehensive study of the statue. This was a two year (1998-1999) project that became the third most important project in terms of press coverage for IBM, after Big Blue (the chess playing machine that beat Kasparof) and the Atlanta Summer Olympics. From IBM’s point of view, in addition to the publicity, the goal of this project was to understand the limitations of relatively inexpensive 3D scanning devices. During this project I developed new surface representations and efficient geometric algorithms to operate on very large polygonal meshes, described somewhere else in this report. My current work on surface reconstruction methods build on these results as a foundation for archaeology and forensic applications.
- A Digital Model of Michelangelo's Florentine Pietà, by F. Bernardini, J. Mittleman, H. Rushmeier, G. Taubin, in 4th Int.l Conf. on Cultural Heritage Networks Hypermedia. Milan, Italy, September 1999.
- Scanning Michelangelo's Florentine Pietà: Making the Results Usable, by F. Bernardini, J. Mittleman, H. Rushmeier, G. Taubin, in Eurographics 99, short papers and demos. Milan, Italy, September 1999.
- Building a Digital Model of Michelangelo's Florentine Pieta', by F. Bernardini, I. Martin, J. Mittleman, H. Rushmeier, and G. Taubin, IEEE Computer Graphics & Applications, January/February 2002.
- The Development of the Virtual Model of Michelangelo’s Florence Pieta, by F. Bernardini, H. Rushmeier, I. Martin, J. Mittleman, and G. Taubin, in Michelangelo’s Florence Pieta, by J. Wasserman, Princeton University Press, 2003.
- The Digital Capture and Virtual Exhibit of Michelangelo’s Piéta, by G. Taubin, in BIRS 2006 Workshop on Mathematical Methods in Computer Vision, Banff International Research Station, Alberta, Canada, September 2006.
TOP
Digital Archaeology / The REVEAL System
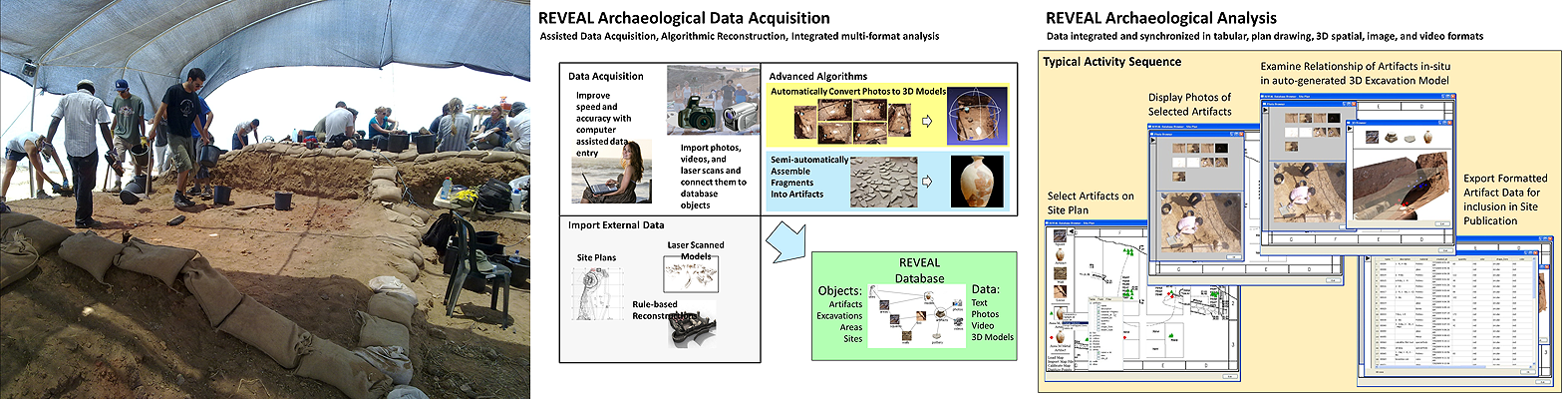
One of the key site-excavation issues is how to locate finds accurately. Traditionally, archaeologists take manual measurements and use hand-drawn sketches, and occasional photographs to record the location of artifacts, layers, and architectural elements. This methodology suffers from inaccuracy, inconsistent terms, transcription errors, and is time consuming. Also, data are sometimes not recorded because their significance is not recognized until too late. Our REVEAL System, currently being tested at many excavations around the world combines multiple modes of input, a back-end database, and a sophisticated user interface to address these issues. This project funded by a large NSF grant, focuses on six fundamental highly interrelated activities: 1) Semiautomatic 3D object and fragment surface and geometry estimation from moving and multiple stationary-image and video-cameras; 2) Automatic reconstruction of objects, especially glass and ceramic, from estimated 3D models of their many fragments; 3) Interactive reconstruction of large architectural structures and archaeological sites; 4) Semiautomatic development of internet accessible archaeological space-time site-database containing both traditional information about findings and images, video, and extracted 3D representations and geometry; 5) 3D immersion for the purposes of collaborative research, making precise metric measurements at an archaeological excavation site from remote locations and interactively manipulating fragments, objects, and architectural substructures to facilitate object and architectural structure reassembly; 6) search tools for pattern-recognition of decorated artifacts or objects based on 2D or 3D geometry, both within a database and across databases at different physical locations.
- NSF IIS program. Title: “III-CXT-Core Computer Vision Research: Promoting Paradigm Shifts in Archaeology” with D.B. Cooper, B.Kimia, and K. Galor. Submitted November 2007. Requested $2,638,964 for four year. Granted $2,638,964, starting in September 2008. Active.
- 3D Slit Scanning with Planar Constraints, by M. Leotta, A. Vandergon, and G. Taubin, Computer Graphics Forum, Volume 27, Number 8, pp. 2066-2080, December 2008.
- One Shot Scanning Using DeBrujin Spaced Grids, by A. Osman Ulusoy, F. Calakli, and G. Taubin, IEEE International Workshop on 3-D Digital Imaging and Modeling (3DIM'09), October 3-4, 2009, Kyoto, Japan
- REVEAL Intermediate Report, by E. Gay, B. Kimia, D.B. Cooper, G. Taubin, D. Sanders, K. Galor, and A. Willis, in Second Workshop on Applications of Computer Vision in Archaeology (ACVA 2010), San Francisco, June 2010.
- Robust One-Shot 3D Scanning Using Loopy Belief Propagation, by F. Calakli, A. Ulusoy, and G. Taubin, in Second Workshop on Applications of Computer Vision in Archaeology (ACVA 2010), San Francisco, June 2010.
- SSD: Smooth Signed Distance Surface Reconstruction, by F. Calakli, and G. Taubin, Pacific Graphics 2011, September 2011.
- SSD: Smooth Signed Distance Surface Reconstruction, by F. Calakli, and G. Taubin, Computer Graphics Forum, vol. 30, no. 7, 2011.
- Smooth Signed Distance Surface Reconstruction, by G. Taubin, Trimester Program on Computational Manifolds and Applications, Instituto Nacional de Matemática Pura e Aplicada (IMPA), Rio de Janeiro, Brazil, October 2011 (invited speaker).
TOP
Dynamic Shape capture / 3D Cinematography
We have recently introduced a novel method to reconstruct the 3D posture of flying bats from sparse synchronized multiple view video. Specifically, we incorporate biomechanical and geometric knowledge about bats into an articulated model. We then estimate the bats time-varying pose by tracking a set of known markers using a Square Root Unscented Kalman filtering method augmented with video optical flow information. Our method scales easily to multiple views, effectively handles missing and occluded markers, and has versatility in the type and complexity of the tracking model. To demonstrate the performance of the reconstruction method, we applied our technique to estimate the parameters of a 52 degree of freedom articulated model of a bat from a real world flight sequence. We further assesed our algorithms performance by quantifying its ability to recover model parameters accurately for a realistic simulated flight sequence. The experiments were done in an enclosed flight corridor with several species of bats. One particular flight sequence that we analyzed was filmed using four calibrated Photron FASTCAM 1024 PCI cameras running at 1000 frames per second. At this frame rate, these cameras record 1024 x 1024 pixel 8-bit grayscale images. We plan to use this technology to implement multi-person tracking algorithms from feature detection and tracking as well as from silhouettes, extending our 3D Photography work into 3D Cinematography.

- Introducing 3D Cinematography, by R. Ronfard and G. Taubin, IEEE Computer Graphics and Applications, May-June 2007, pp. 18-20.
- Image and Geometry Processing for 3-D Cinematography: An Introduction, by Remi Ronfard and Gabriel Taubin (eds.), Springer-Verlag, 2010, ISBN: 978-3-642-12391-7.
- Falling with Style-Bat Flight Maneuvers, by A. Bergou, D. Riskin, G. Taubin, S. Swartz, and K. Breuer, Bulletin of the American Physical Society, Vol. 55, 2010.
- Inertial and Fluid Forces during Bat Flight Maneuvers, by A. Bergou, J. Franck, G. Taubin, S. Swartz, and K. Breuer, Bulletin of the American Physical Society, Vol. 56, 2011.
- Falling with Style: The Role of Wing Inertia in Bat Flight Maneuvers, by A.J. Bergou, D.K. Riskin, G. Taubin, S.M. Swartz, and K. Breuer, The Society for Integrative & Comparative Biology 2011 Meeting, Salt Lake City, UT, Jan. 3-7, 2011.
- 3D Reconstruction and Analysis of Bat Flight Maneuvers from Sparse Multiple View Video, by A. Bergou, S. Swartz, S. K. Breuer, G. Taubin, Proceedings of the 1st IEEE Symposium on Biological Data Visualization, Providence, RI, October 2011.
- 3D Reconstruction of Bat Flight Kinematics from Sparse Multiple Views, by A. Bergou, S. Swartz, and G. Taubin, and K. Breuer, Proceedings of the 1st IEEE International Workshop on Dynamic Shape Capture and Analysis (4DMOD), Barcelona, Spain, November 2011.
- NSF IIS Core Program, Medium Project, Title: “CGV: Medium: Representing 3D Scenes as Distributions of Oriented Points,” G.Taubin (PI), J. Mundy (co-PI). Submitted September 2011 (pending).
TOP
Interaction and Large Format Displays

In a dense stereo algorithm, two previously calibrated cameras are used to estimate the 3D depth (position) of each pixel of a reference image. A stereo algorithm efficiently searches for geometric correspondence between pairs of pixels in the two images along epipolar lines, resulting in a depth estimate for each pixel. In We introduced a new GPGPU-based real-time high-resolution high frame rate dense stereo matching algorithm was introduced. It is based on a progressive multi-resolution pipeline which includes background modeling and dense matching with adaptive windows. For applications in which only moving objects are of interest, this approach effectively reduces the overall computational cost quite significantly, and preserves the high definition details. Running on an off-the-shelf NVIDIA graphics card, our first implementation achieved 7200M disparity evaluations per second. Included in this figure is all the overhead associated with downloading images to the graphics hardware and uploading disparity maps. This implementation achieved 60 fps stereo matching on 800x600 stereo video with a fine 250 pixels disparity range. At the time, these results outperformed all published alternative algorithms, including GPU-based implementations, by a large margin. In our implementation only the GPU is used for processing the video data. Therefore the CPU power is free to perform other tasks. This stereo system constitutes an alternative to the popular and inexpensive Microsoft Kinect RGB-D camera, which we are also using in various projects. However, while the Kinect sensor cannot be used in many multi-view applications because it is an active illumination device, this system, based on passive illumination can scale up to the proposed multi camera unit system with large numbers of stereo cameras. Performance will be improved by projecting a static high frequency pattern onto the scene to increase the texture content in the infrared band.
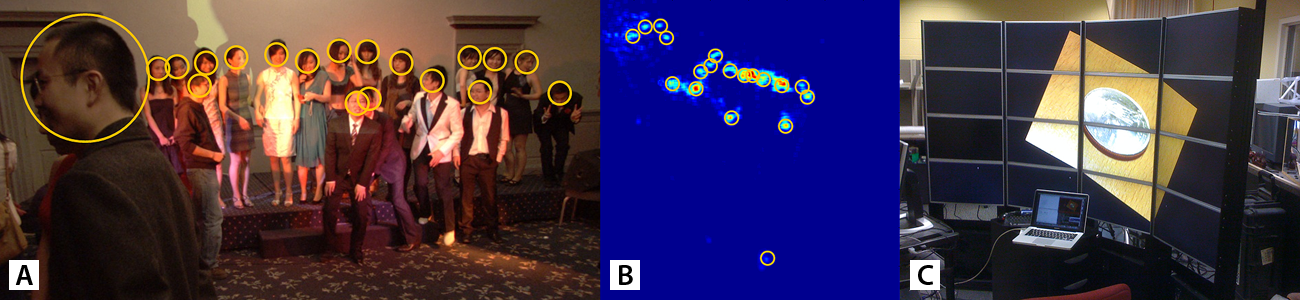
Leveraging our GPGPU-based real-time high-resolution high frame rate dense stereo matching algorithm, we developed a novel real-time-stereo-based people identification and tracking algorithm which detects people on a plan-view occupancy map. The 3D measurement of objects is used to select stable and distinctive local features and enhance feature descriptors with 3D characteristics. A dedicated feature matching framework was designed in such a way that it not only considers a person's appearance, but also his or her physical size, position, and the relations existing amongst different features. A distinctive object descriptor was proposed based on these 3D-enhanced local features. This new object descriptor can be used to identify non-rigid objects in a sparse visual sensor network. Experimental results show that this new algorithm achieves very high performance on identifying walking people. Here we propose to extend these technique by: 1) using multiple synchronized stereo cameras to cover a wider field of view; 2) combine the depth data produced by all the stereo cameras in a common coordinate system and estimate a dynamic shape updated at frame-rate; 3) analyze the geometry described by the dynamic shape to detect and track individuals; and 4) use the output of this system to control processes and visualizations being rendered in a large format display, such as the video wall shown in the figure above.
- INRIA Associate Teams Program for International Cooperation. Title: “Video and Mesh Processing for 3D Cinematography (VAMP);” with C. Jenkins (Brown-CS), R. Ronfard (INRIA), E. Boyer (INRIA), and F. Devernay (INRIA). Granted on December 2004. Renewed in December 2005 and in December 2006.
- NSF OISE Number 0553462. Title “International Research Experiences for U.S. Students at INRIA;” PI: Victor Vianu (UCSD). Includes travel support for students from 14 US institutions for three years. 2006-2009.
- Real-Time Median Filtering for Embedded Smart Cameras, by Y. Zhao and G. Taubin, IEEE International Conference on Computer Vision Systems, St. Johns University, Manhattan, New York City, January 2006
- DARPA Seedling grant, “Real-Time Aerial Exploitation;” with J. Mundy and D.B. Cooper. July-2006-September 2008.
- NSF Networking Technology and Systems (NeTS) Networking of Sensor Systems (NOSS) program NSF-05-505. Title: “NeTS-NOSS: Sensing Three Dimensions with Smart Cameras;” with Ugur Cetintemel (Brown-CS) and John Jannotti (Brown-CS). Submitted January, 2007. Requested $972,705 for three years. Granted $700,000. September 2007 – August 2011.
- Parallax-Free Aerial Video Registration, by D. Crispell, J. Mundy, and G.Taubin, British Machine Vision Conference 2008, BMVC’08.
- Data-Centric Visual Sensor Networks for 3D Sensing, by M. Akdere, U. Centintemel, D. Crispell, J. Jannottii, J. Mao, and G. Taubin, Second International Conference on GeoSensor Networks 2006, GSN 2006, Lecture Notes in Computer Sciences (LNCS), Vol 4540, pp. 131-150, 2008.
- Real-Time High Definition Stereo on GPGPU using Progressive Multi-Resolution Adaptive Windows, by Y. Zhao, and G. Taubin, NVIDIA Research Summit 2009, NVIDIA GPU Technology Conference, October 2009.
- Office of the Vice-President for Research, Research Seed Grant, Title: “Advancing Digital Scholarship with Touch‐Surfaces and Large‐Format Interactive Display Walls.” G. Taubin(PI), Andy van Dam (CS, co-PI), Harriette Hemmasi (University Librarian, co-PI), and M. Riva (Italian Studies, co-PI). Granted January 2010. Active.
- Detection, Tracking, and Identification of Humans using Stereo Vision, Y. Zhao, PhD thesis, Brown University, 2010 (Taubin, advisor).
- Real-Time Stereo on GPGPU Using Progressive Multi-Resolution Adaptive Windows, by Y. Zhao and G. Taubin, chapter in GPU Computing Gems, Morgan Kaufmann, January 2011.
- Real-Time High-Definition Stereo on GPGPU using Progressive Multi-Resolution Adaptive Windows, by Y. Zhao, and G. Taubin, Image and Vision Computing, Volume 29 Issue 6, May, 2011.
- Using stereo vision to detect, track and identify people, by Y. Zhao and G. Taubin, IEEE Communications Society, Multimedia Communications Technical Committee E-Letter, June 2011.
- NSF CISE Computing Research Infrastructure (CRI), Title “II-NEW: Development of a Large-Scale Real-Time Dynamic Shape and Motion Capture Studio,” G. Taubin (PI), and T. Winkler (co-PI). Submitted October 2011 (under review).
TOP
Medical Imaging and Medical Devices
In collaboration with local industry partners and members of Brown Medical School I am currently pursuing a number of 3D shape capture and visualization applications of my technology, in particular in the area of endoscopic surgery. For example, I am collaborating with Lucidux, inc. in the development of a new 3D endoscope. In early work at IBM, I collaborated with the Computed Assisted Surgery group, helping in the development of the 3D graphics software used in their Hip Replacement Revision Surgery Planning System funded by a NIST ATP Grant. I plan to continue actively exploring applications of my technology in this domain.
- Rhode Island STAC, Title: “Early Cancer Detection and Treatment using Advanced Three-Dimensional Surface Texture Visualization and Modeling.” G. Taubin (PI), J. Harry (Lucidux Corp., co-PI), G. Haleblian (Brown Medical School, co-PI), G. Pareek (Brown Medical School, co-PI). Started February 2010. Active.
- NIH NIBIB SBIR, Title: “Lung Nodule Detection using 3D visual palpation via standard thoracoscopes” J. Harry (Lucidux Corp., PI), F. Luks (Lifespan/Rhode Island Hospital, co-PI), D. Gnepp (Lifespan/Rhode Island Hospital, co-PI), G. Taubin (consultant). Submitted August 2010, revised December 2010, granted 2011. Started Fall 2011.
- Rhode Island STAC, Title: “Interactive Multi-User Display System for Laparoscopic Surgery.”Francois Luks, (Lifespan/Rhode Island Hospital/Medical School, PI) G. Taubin (co-PI). To be re-submitted November 2011.
- Computer Integrated Revision Total Hip Replacement Surgery: Preliminary Results, by L. Joskowicz, R.H. Taylor, B. Williamson, R. Kane, A. Kalvin, A. Gueziec, G. Taubin, J. Funda, S. Gomory, L. Brown, and J. McCarthy, Second Int. Symposium on Medical Robotics and Computer-Assisted Surgery (MRCAS '95), Baltimore, Nov. 5-7, 1995
