Assignment 2: Linear and Nonlinear Filters
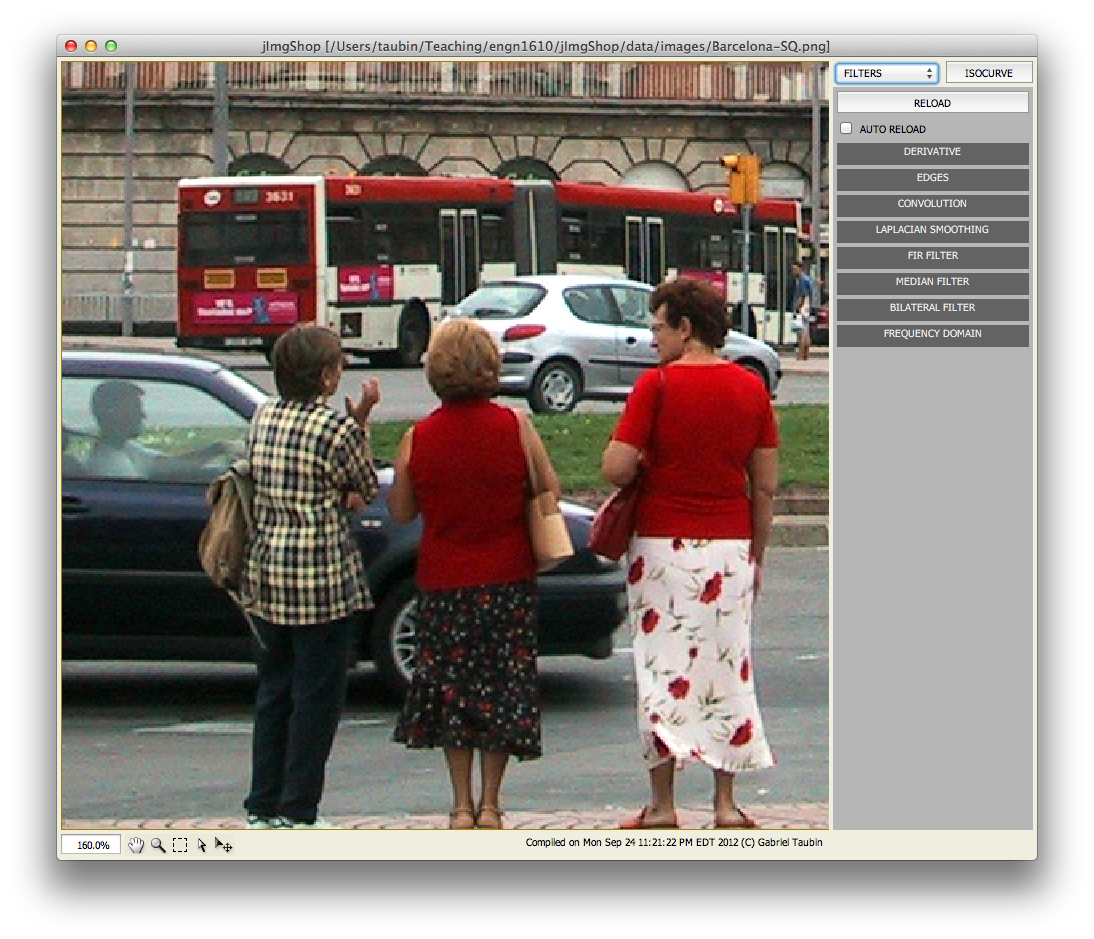
The goal of this assignment is to implement several linear and nonlinear image filters.
DATES
This assignment, comprising directional derivative, Sobel and Roberts edge detectors, Laplacian smoothing, FIR Filters, convolution, median, and bilateral filters, is out on Monday, September 28, 2012, and it is due on Monday, October 8, 2012.
ASSIGNMENT FILES
Download the zip file ENGN1610-2012-A2.zip containing all the Assignment 2 files. Unzip it to a location of your choice. You should have now a directory named assignment2 containing the following five files
- Makeflie
- JImgShopA2.zip
- JImgShopA2.lnk
- JImgPanelPixelOps.java
- ImgPixelOps.java
- JImgPanelFilters.java
- ImgFilters.java
- javac -O -classpath ".;JImgShopA2.zip" JImgPanelFilters.java
- javac -O -classpath ".;JImgShopA2.zip" JImgPanelPixelOps.java
- JImgPanelFilters.class
- ImgFilters.class
- JImgPanelPixelOps.class
- ImgPixelOps.class
In a windows machine you can run the JImgShop program by double clicking on the shortcut JImgShopA2.lnk. Otherwise, type the following command at a command promp.
- java -Xmx1000M -cp ".;jImgShopA2.zip" JImgShopApp -w 790 -h 800 -st
The file JImgPanelFilters.java contains the implementation of the graphical user interface associated with this assignment. You don't need to edit this file unless you want to modify the design of the GUI. However, you may want to study it to understand how the functions that you need to implement will be called.
The file ImgFilters.java contains the implementation of the class ImgFilters, which is designed to isolate the Linear and Nonlinear Filter Operations from the rest of the program. The class ImgFilters comprises the following public methods
- public Img directionalDerivative(float angDegrees)
- public Img sobelEdges()
- public Img robertsEdges()
- public Img laplacianSmoothing(float lambda, int n)
- public Img firFilter(float[] f);
- public Img convolution(float[] h)
- public Img median(int N);
- public Img bilateral(float sigmaSpace, float sigmaRange)
- public Img applyFrequencyDomainFilter(VecFloat frequencyResponse)
THE ImgFilters CLASS
For this assignment you need to complete the implementation of this class.
public Img directionalDerivative(float angDegrees)
In this method you will implement a directional derivative filter for an arbitrary direction specified by the parameter angleDegrees. We define this directional derivative as a linear combination of the central difference with respect to the x direction and the central difference with respect to the y direction of the intensity of the input image, with linear combination cefficients equal to the cosine and sine of the angle, respectively. Since this computation results in pixel values in the range [-255:255] which cannot be represented in our images, you need to linearly map the resulting pixel values to the desired range scale [0:255]. The output image should be set as monochrome, with the red, green, and blue channels holding the same values. For pixels on the first border rows and columns you should implement mirror symmetric constraints.
An alternative implementation, which does not require much additional works is to evaluate the directional derivative as defined above for the red, green, and blue channels independently, and set the results in the red, green, and blue channels of the output image. You may implement this version insted, or even better, add a Checkbox to the user interface to let the user select which of the two versions will be run. In both cases, copy the alpha channel from the source image, or just set it to 0xff.
public Img sobelEdges()
Please read the definition of the Sobel Operator from Wikipedia http://en.wikipedia.org/wiki/Sobel_operator You have the choice of evaluating the Sobel Operator on the intensity of the input image, or on the three channels independently. In the first case you should set the output as a monochrome image with the red, green, and blue channels of each pixel holding identical numerical values. If you evaluate the three channels independently, you may either set the three channels of the output image independently, or combine the three values as the root mean square value of the red, green, and blue values. Structure your code so that all these options could be implemented with minimal changes to the code. Another alternative would be to implement the Scharr Opeartor instead of the Sobel Operator. Read about the Scharr Operator in the Wikipedia mentioned above. You may also want to modify the user interface to give the user all these choices. In all cases, copy the alpha channel from the source image, or just set it to 0xff.
public Img robertsEdges()
Please read the definition of the Roberts Operator from Wikipedia http://en.wikipedia.org/wiki/Roberts_Cross The same considerations as for the Sobel Operator apply to the Roberts Operator. Structure your code to minimize the amount of additional code necessary to implement the Roberts Operator from the implemenation of the Sobel Operator.
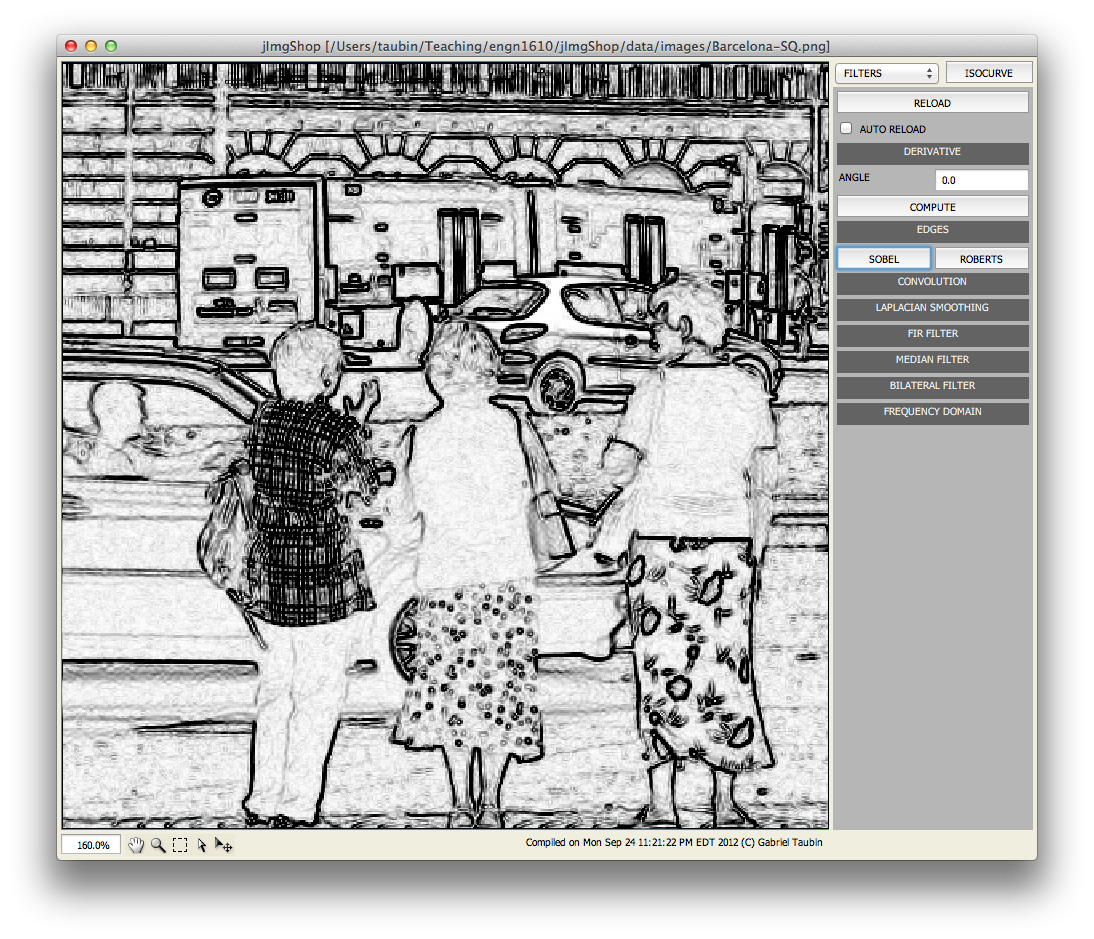
public Img laplacianSmoothing(float lambda, int n)
Laplacian Smoothing is an operation which is normally applied to polygon meshes. But it can be applied to images as well, and since it is extremely simple and it provides a basic mechanism to implement arbitrary filters with polynomial transfer function in the space domain, we are going to implement it here.
The Laplacian Operator applied to an image results in another image of the same dimensions where each pixel value is equal to the average of the differences of neighboring pixels with respect to the given pixel. After the Laplacian Operator is computed as a function of the input image, it should be scaled by the parameter lambda and added the the input image pixel by pixel. The process can then be repated, with parameter n specifying the number of iterations. For a color image, the process should be applied to each color channel independently. A new ImgFloat class is provided to represent monochrome images as arrays of floating point variables. Structure your code so that the Laplacian Operator is implemented as a separate private funtion operting on an instance of the ImgFloat class, and returning the result in a second instance of the same class. The public method should extract the three channels from the input image, convert them to instances of the ImgFloat class, apply the desired number of Laplacian Smoothing steps, convert the three resulting channels from float to int, making sure that overflow and underflow is prevented, and set the three channels of the output image. In all cases, copy the alpha channel from the source image, or just set it to 0xff.
public Img firFilter(float[] f);
In Signal Processing a Finite Impulse Response (FIR) filter is a recursive filter with polynomial transfer function. Here we refer to FIR Filter as a filter defined by a univariate polynomial defined by the vector of coefficient f applied to the Laplacian Operator. If you properly structure you implementation of Laplacian Smoothing, this task should be straighforward.
public Img convolution(float[] h)
In this method you will implement a convolution filter. The linear array h contains the coefficients of the two dimensional impulse response in the range [-2:2]x[-2:2] organized in scan order. For pixels on the first two border rows and columns you should implement mirror symmetric constraints. Filter the red, gree, and blue channels independently. Copy the alpha channel from the source image.
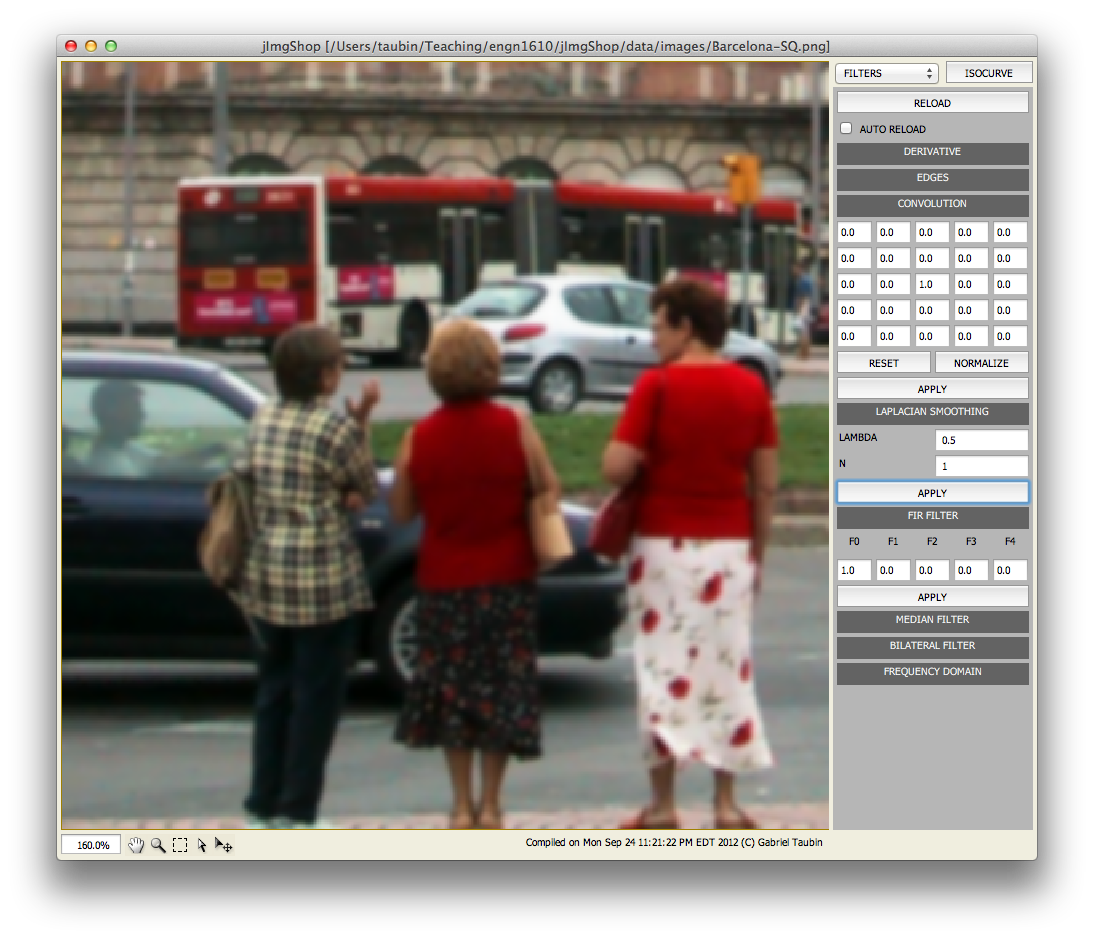
public Img median(int N)
In this method you will implement a median filter. The parameter N defines the pixel neighborhood [-N:N] over which the median needs to be computedx[-N:N]. For pixels on the first N border rows and columns you should implement mirror symmetric constraints. Filter the red, gree, and blue channels independently. Copy the alpha channel from the source image.
public Img bilateral(float sigmaSpace, float sigmaRange)
In this method you will implement a bilateral filter defined by the two parameters sigmaSpace and sigmaRange. For pixels close to the border you should implement mirror symmetric constraints. Filter the red, gree, and blue channels independently. Copy the alpha channel from the source image.
Read A Gentle Introduction to Bilateral Filtering and its Applications by S. Paris, P. Kornprobst, J. Tumblin, and F. Durand, and select one of the many variants. If you decide to implement a version that requires more parameters, then modify the user interface to be able to specify those parameters.
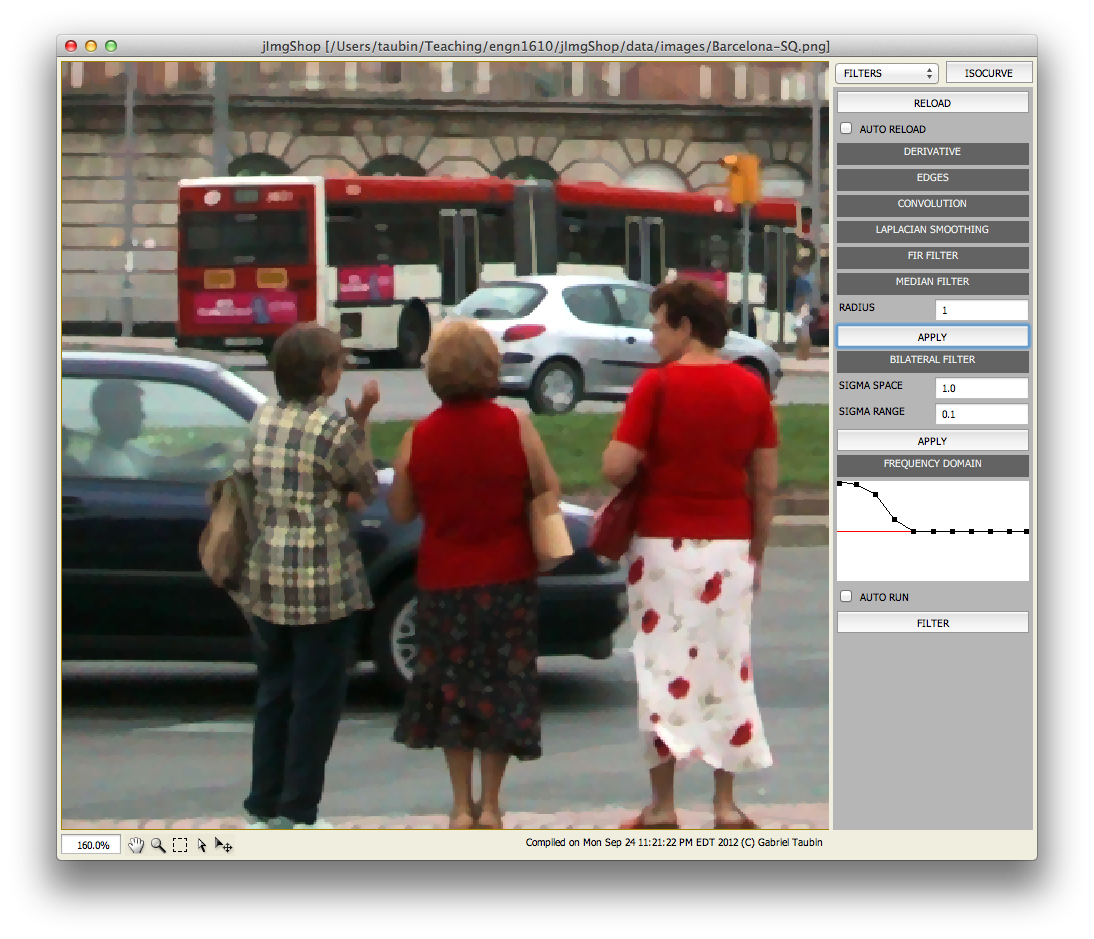
public Img applyFrequencyDomainFilter(VecFloat frequencyResponse)
In this method you will implement a linear filter in the frequency domain. To transform the image to the frencuency domain you will implement the discrtete time cosine transform for one dimensional discrete N-dimensional signals, which you will use to implement the discrete time cosine transform for digital images. The argument is a vector of (float key, float value) pairs representing the frequency response of the filter as a piecewise linear function. The key variables are guaranteed to be provided sorted in non-decreasing order, with the first equal to 0.0, and the last equal to 1.0. Scaling of the frequency variable is required to map frequency indices onto the [0.0:1.0] range. The value variables may hold arbitrary values.
private void _discreteCosineTransform(ImgFloat imgSrc, ImgFloat imgDst)
In this method you will implement the discrete cosine transform of an image composed of one dimensional float pixel values. You first need to compute the one dimensional discrete time cosine transform of each row, and store the results in place. Then you need to compute the one dimensional discrete time cosine transform of each column, and store the results in place.
private void _dtct(float[] x, float[] X)
In this method you will implement the discrete time cosine transform of a one dimensional signal x. You should store the result in the array X.
WHAT TO SUBMIT
You need to submit your edited file ImgFilters.java. Make sure that it is well commented out. Explain all your choices in the comments. If you were not able to make somethig work, explain the problems here. If you modify the user interface, then you also need to submit your edited JImgFilters.java file. If you need to explain things with formulas, you can also send us a document. Create a zip file named ENGN1610-A2-NAME.zip and send it to the instructor as an attachment, where NAME is your last name.