Assignment 3:
Geometric Transformations, Polygon Mesh Warping,
and Polygon Mesh Generation
The goal of this assignment is to implement several geometric transformations: affine, bilinear, and projective; warping transformations based on polygon mesh deformations: picewise linear and piecewise bilinear; and some mesh generation algorithgms: adaptive triangle mesh subdivision and laplacian smoothing.
DATES
The assignment is out on Tuesday, October 16, 2012, and it is due on Monday, October 29, 2012.
ASSIGNMENT FILES
Download the zip file ENGN1610-2012-A3.zip containing all the Assignment 3 files. Unzip it to a location of your choice. You should have now a directory named assignment3 containing the following five files
- Makeflie
- JImgShopA3.zip
- JImgShopA3.lnk
- JImgPanelPixelOps.java
- ImgPixelOps.java
- JImgPanelFilters.java
- ImgFilters.java
- JImgPanelWarping.java
- ImgWarping.java
- Mesh.java
- javac -O -classpath ".;JImgShopA3.zip" JImgPanelWarping.java
- javac -O -classpath ".;JImgShopA3.zip" JImgPanelFilters.java
- javac -O -classpath ".;JImgShopA3.zip" JImgPanelPixelOps.java
- JImgPanelWarping.class
- ImgWarping.class
- Mesh.class
- JImgPanelFilters.class
- ImgFilters.class
- JImgPanelPixelOps.class
- ImgPixelOps.class
In a windows machine you can run the JImgShop program by double clicking on the shortcut JImgShopA3.lnk. Otherwise, type the following command at a command promp.
- java -Xmx1000M -cp ".;jImgShopA3.zip" JImgShopApp -w 790 -h 800 -st
The file JImgPanelWarping.java contains the implementation of the graphical user interface associated with this assignment. You don't need to modify this file unless you want to modify the design of the GUI.
The file ImgWarping.java contains the implementation of the class ImgWarping, which is designed to isolate the geometric transformations that you need to implement from the rest of the program. In the class ImgWarping you need to implement the following public methods
- public Img affineTransformation(Mesh mesh, Img dstImg);
- public Img bilinearTransformation(Mesh mesh, Img dstImg);
- public Img projectiveTransformation(Mesh mesh, Img dstImg);
- public Img piecewiseLinearTransformation(Mesh mesh, Img dstImg);
- public Img piecewiseBilinearTransformation(Mesh mesh, Img dstImg);
The file Mesh.java contains a partial implementation of the class Mesh, which is designed to isolate the mesh generation and manipulation operations that you need to implement from the rest of the program. In the class Mesh you need to implement the following public methods
- public void subdivide();
- public void laplacianSmoothing
(float lambda, int n, boolean smoothSrc, boolean smoothDst, boolean fixSelected);
THE ImgWarping CLASS
For this assignment you need to complete the implementation of this class.
public Img affineTransformation(Mesh mesh, Img dstImg)

In this method you will implement an affine transformation \(q=A\,p+b\), where \[ q=\left[\matrix{u_0\cr u_1}\right]\quad A=\left[\matrix{a_{00} & a_{01}\cr a_{10} & a_{11}}\right]\quad p=\left[\matrix{x_0\cr x_1}\right]\quad\hbox{and}\quad b=\left[\matrix{b_0\cr b_1}\right]\quad, \] defined by two corresponding triangles, one in the source image \(\{p_0,p_1,p_2\}\), and another on the destination image \(\{q_0,q_1,q_2\}\), so that \(q_j=A\,p_j+b\) for \(j=0,1,2\).
For each pixel \(q\) in the destination image, compute the barycentric coordinates \(\lambda=(\lambda_0, \lambda_1,\lambda_2)^t\) of the pixel location with repect to the destination triangle so that \begin{equation} \left[\matrix{q\cr 1}\right]= \lambda_0\, \left[\matrix{q_0\cr 1}\right] + \lambda_1\, \left[\matrix{q_1\cr 1}\right] + \lambda_2\, \left[\matrix{q_2\cr 1}\right] = \left[\matrix{ q_0 & q_1 & q_2\cr 1 & 1 & 1 }\right] \, \left[\matrix{ \lambda_0\cr \lambda_1\cr \lambda_2 }\right] \label{eq:affine} \end{equation} Determine the location of the pixel location in the source image with the same barycentric coordinates with respect to the source triangle \[ p=\lambda_0\,p_0+\lambda_1\,p_1+\lambda_2\,p_2 \] and set the destination pixel color to the value obtained by sampling the source image at the computed source pixel location.
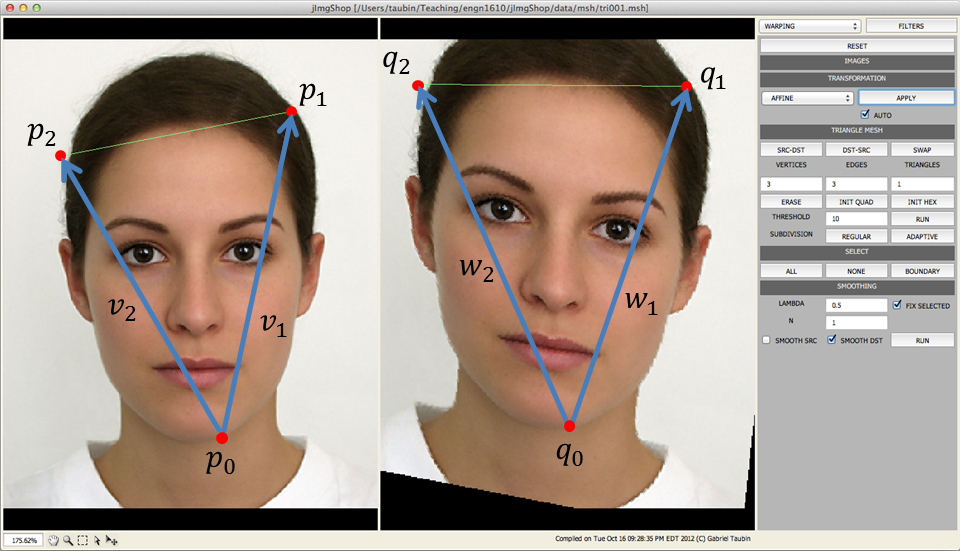
If the transformation is contracting, prefiltering is necessary to prevent aliasing. If the transformation is expanding, postfiltering is necessary to prevent pixelation efects. Alternatively, higher order interpolation can be used. Feel free to experiment with all these variations.
public Img bilinearTransformation(Mesh mesh, Img dstImg)

In this method you will implement a bilinear transformation defined by two corresponding quadrilaterals; one on the source image, and another on the destination image. For each pixel in the destination image, compute the bilinear coordinates of the pixel location with repect to the destination quadrilateral; determine the location of the pixel location in the source image with the same bilinear coordinates with respect to the source quadrilateral; and set the destination pixel color to the value obtained by sampling the source image at the computed source pixel location. The same considerations about pre and post filtering apply here.
public Img projectiveTransformation(Mesh mesh, Img dstImg)

As in the bilinear transformation case, in this method you will implement a projective transformation defined by two corresponding quadrilaterals; one on the source image, and another on the destination image.
public Img piecewiseLinearTransformation(Mesh mesh, Img dstImg)

In this method you will implement a picewise linear transformation deined by a triangular mesh with different vertex coordinates on the source and destination images. The deformed mesh results in a different affine transformation applied to the pixels contained within each triangle. The core computation in this method is the same as in the affine transformation.
public Img piecewiseBilinearTransformation(Mesh mesh, Img dstImg)
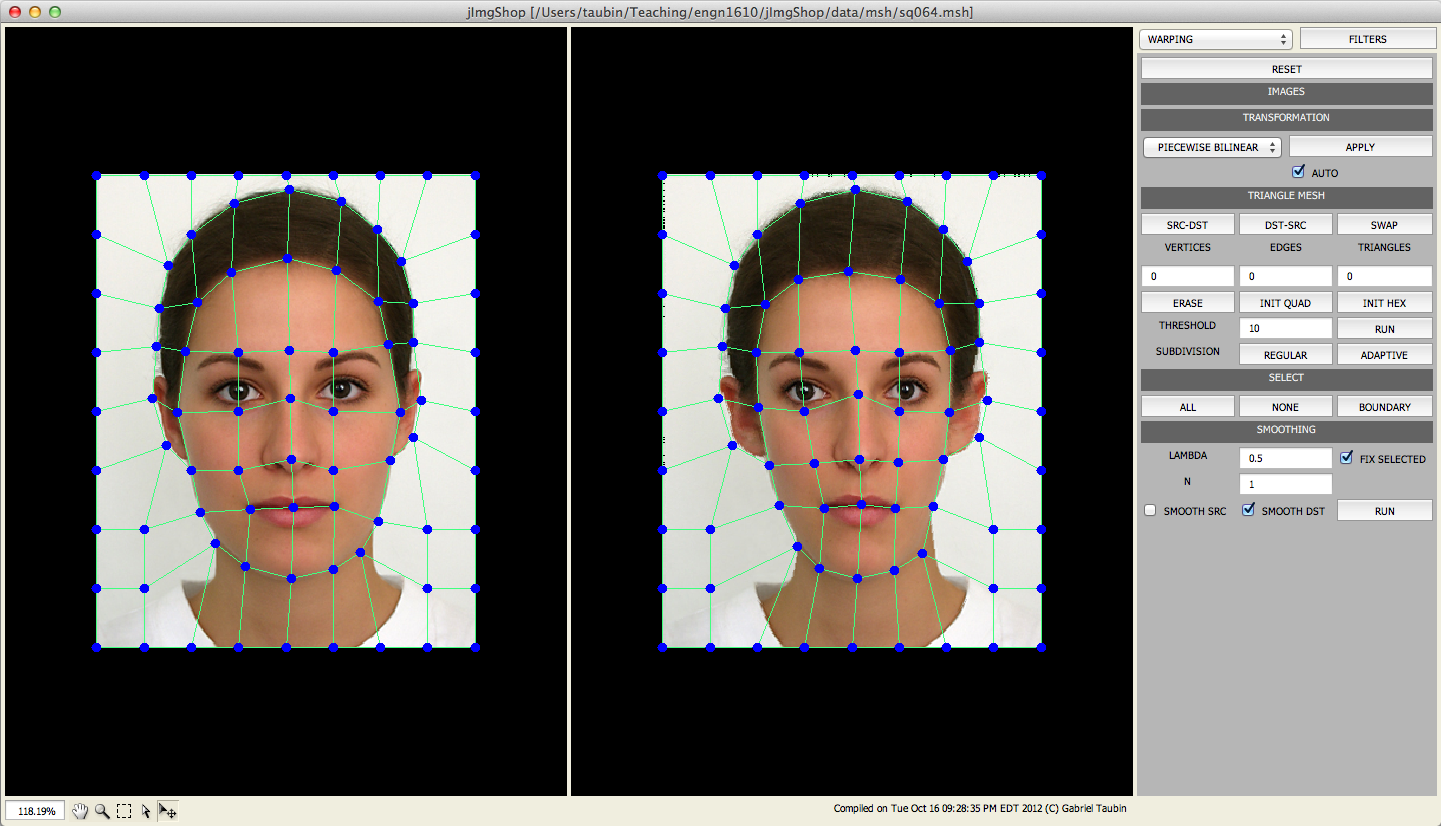
In this method you will implement a picewise bilinear transformation deined by a quadrilateral mesh with different vertex coordinates on the source and destination images. The deformed mesh results in a different bilinear transformations applied to the pixels contained within each quadrilateral. The core computation in this method is the same as in the bilinear transformation.
THE Mesh CLASS
For this assignment you need to complete the implementation of this class.
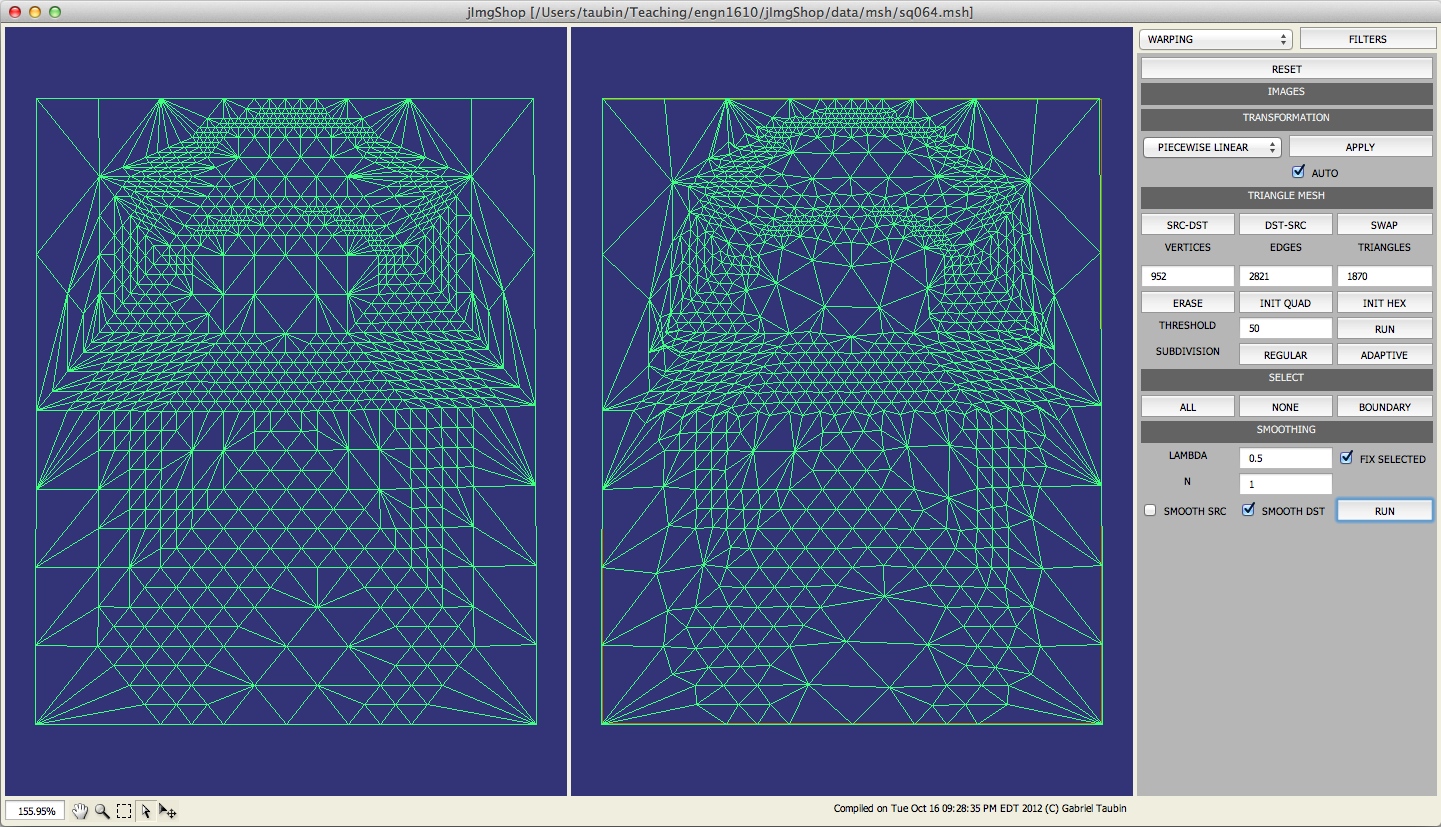
public void subdivide()

In this method you will implement the red-blue triangle mesh subdivision method, which comprises the following steps: 1) paint all the vertices blue; 2) decide which triangles need to be subdivided; 3) for each triangle that needs to be subdivided, paint its vertices red; 4) split each edge with the two vertices painted red; 5) split each triangle with two vertices painted red into two triangles, and each triangle with the three vertices painted red into four triangles.
public void laplacianSmoothing
(float lambda, int n, boolean smoothSrc, boolean smoothDst, boolean fixSelected)
In this method you will implement Laplacian smoothing for polygon meshes. The same method that you implemented in assignment 2 can be modified to work in this case. If \(x_i\) representes the 2D coordinates of the \(i\)-th vertex of the mesh, then the new position of this vertex are computed as \[ \begin{aligned} x_i' = x_i+\lambda \Delta x_i \end{aligned} \] where \(0<\lambda<1\), \(i^\star\) is the set of vertices \(j\) connected to vertex \(i\) by and edge \((i,j)\), and \(|i^\star|\) is the number of elements in the set \(i^\star\) \[ \begin{aligned} \Delta x_i = \frac{1}{|i^\star|} \sum_{j\in i^\star} (x_j-x_i) \end{aligned} \]