Meetings

MWF 2:00-2:50


ASSIGNMENT 4
FILES


DATES
OUT ON WED OCT 31
DUE ON MON NOV 12

Assignment 4:
Computing Isocurves and Smoothing Polygon Curves


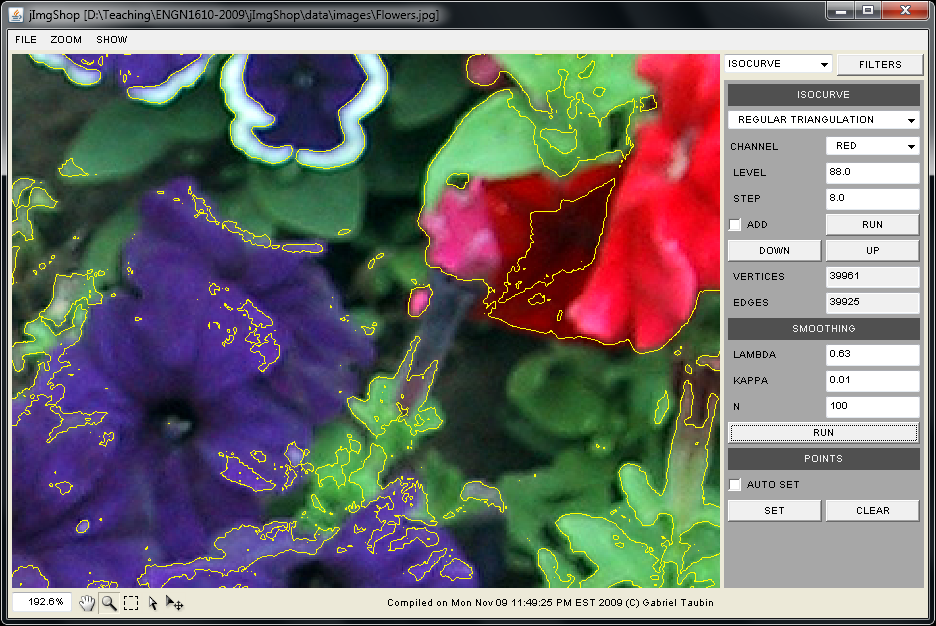
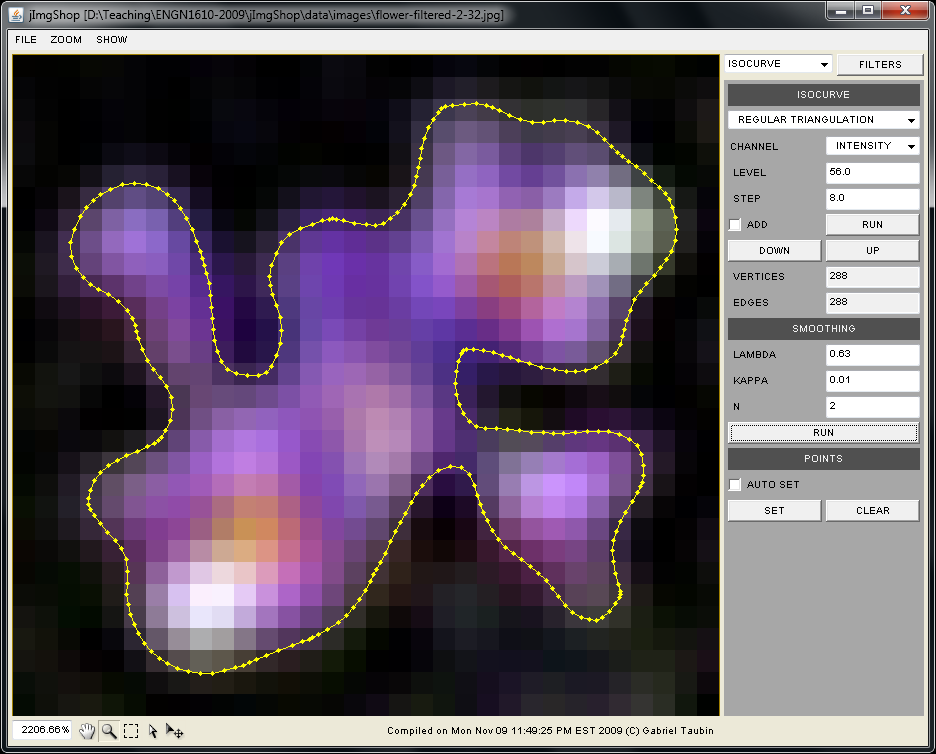
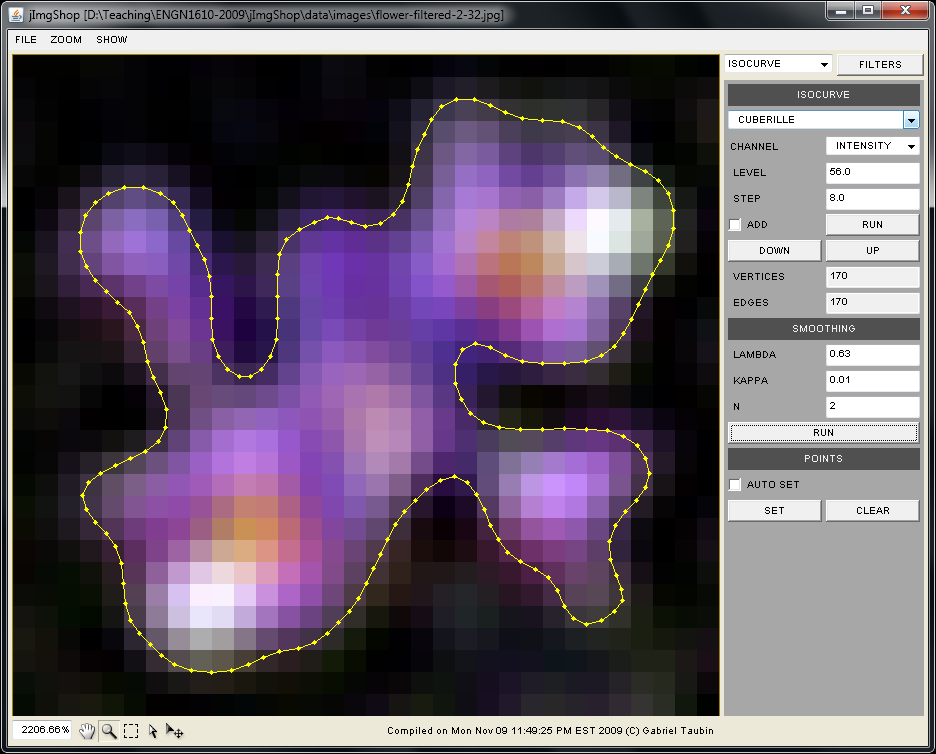
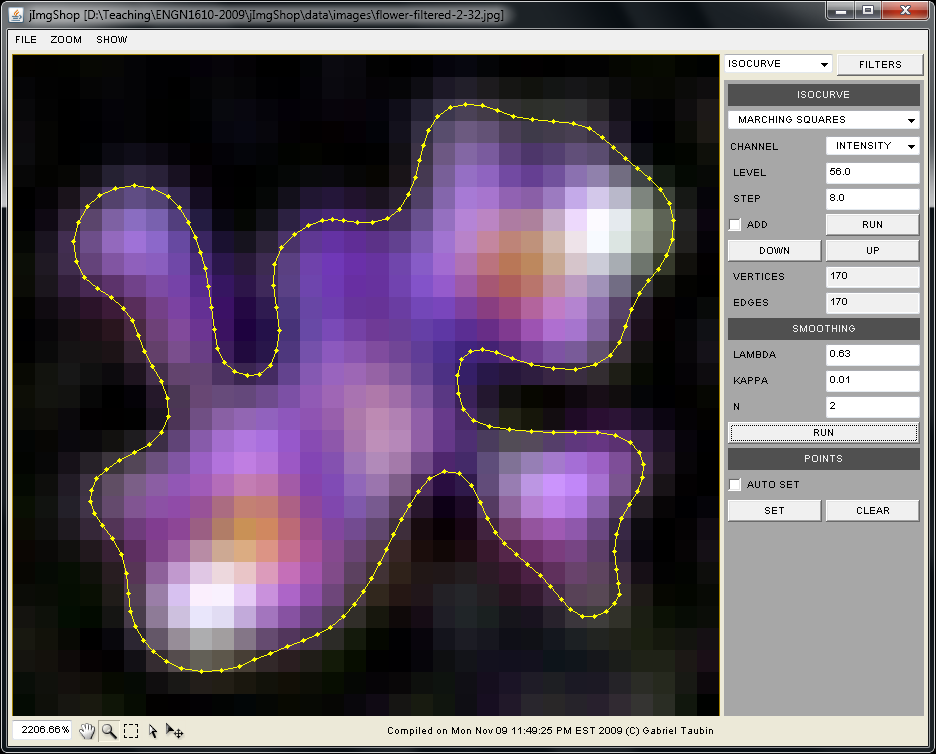
The goal of this assignment is to implement several isocurve extraction algorithms: regular triangulation, cuberille, and marching squares; as well as a simple smoothing algorithm for polygonal curves.

DATES

The assignment is out on Wednesday, October 31, 2012, and it is due on Monday, November 12, 2012.

ASSIGNMENT FILES

Download the zip file ENGN1610-2012-A4.zip containing all the Assignment 4 files. Unzip it to a location of your choice. You should have now a directory named assignment4 containing the following five files

You shuld replace ImgPixelOps.java, ImgFilters.java, and ImgWarping.java with your own versions from Assignments 1, 2, and 3. As in previous assignments, the Makefile is used to automate the compilation process. Otherwise, you can run the following commands at a command prompt in the same directory If the compilation runs without errors, you should find the following new files in the same directory These are compiled Java bytecode files. The JImgShop program requires these files and the zip file JImgShopA4.zip to run. The zip file JImgShopA4.zip contains the rest of the Java bytecode files that the JImgShop program requires to run.

In a windows machine you can run the JImgShop program by double clicking on the shortcut JImgShopA4.lnk. Otherwise, type the following command at a command promp.

To speed-up the process you can create a script file to run the previous command.

The file JImgPanelIsocurve.java contains the implementation of the graphical user interface associated with this assignment. You don't need to modify this file unless you want to modify the design of the GUI.

THE ImgIsocurve CLASS

The file ImgIsocurve.java contains the implementation of the class ImgIsocurve, which is designed to isolate the isocurve and polygon smoothing algorithms that you need to implement from the rest of the program. The class ImgIsocurve includes the following public methods already implemented and the following ones which you need to implement.

As provided, the class also includes a number of protected and private methods which should be regarded as hints. Feel free to delete those methods if you decide to implement your code in a different way.

THE GraphPlanar CLASS

This class, which extends the Graph class, is used to represent planar polygonal curves in indexed form. Every vertex of a polygonal curve has two coordinates and an index. The coordinates are stored in a linear array, and the indices correspond to locations within this array. Edges connect pairs of vertices. Each edge is represented as a pair of vertex indices. A Graph may be oriented or directed. In this assignment we will use directed graphs, to differentiate between the inside from the outside of closed curves.

The application takes care of creating an instance of the GraphPlanar class for us to use to store isocurves extracted from images. The method resets a given instance of the GraphPlanar class to the empty state, and establishes whether the curve to be created by adding vertices and edges will be oriented or not. You cannot change the orienation type once vertices and edges have been added to the curve.

The method returns an instance of the VecFloat class (introduced in assignment 1), which contains the linear array of 2D vertex coordinates. The method returns the total number of 2D vertices currently stored in this array. To add a new vertex, you can use the following method which returns the vertex index of the new vertex. Remember that these coordinates are scaled so that the vertex coordinate range [0.0:1.0]x[0.0:1.0] maps onto the pixel range [0:width]x[0:height].

Edges are pairs of vertex indices. To add a new edge, you can use the following method If the graph is oriented, the order in which the two vertex indices are passed to this method is important, since the edge (iV0,iV1) is regarded as different from the edge (iV1,iV0).

The method retrieves an edge previously created. If such an edge is found, it returns an instance of the GraphEdge class. If the edge is not found, it return null. Edges are stored internally as linked lists, which allows for linear traversal of all the edges. The GraphEdge class includes the following methods where the argument of getVertex() can only be 0 or 1. As edges are created they are assigned consecutive indices. The method getIndex() is used to retrieve those indices, which can be used to map edges onto other properties stored in external data structures, such as arrays.

To linearly traverse the edges you should use the following code structure 

   Graph g;
   GraphEdge e;
   for(int i=0;i<g.getNumberOfVertices();i++) {
     for(e=g.getFirstEdge(i);e!=null;e=g.getNextEdge(e)) {
       int iE  = e.getIndex();
       int iV0 = e.getVertex(0);
       int iV1 = e.getVertex(1);
       // ...
     }
   }

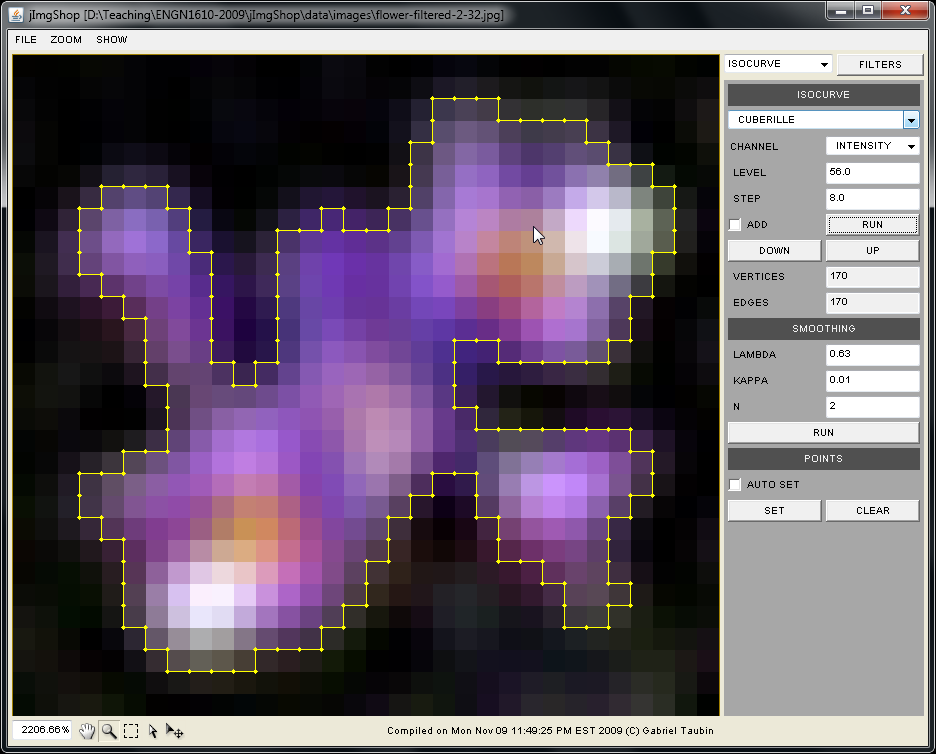
  • public void computeCuberille(float level)



    In this method the isocurve vertices are located at corners of image pixels, and the isocurve edges are some of the image edges shared by neighboring pixels. The algorithm runs in linear time and can be implemented with four image scans.


    In the first scan a binary image is produced. Each image pixel value is tested against the desired isocurve level. If the image pixel value is larger than the isovalue the binary pixel value is set to 1; otherwise it is set to 0.

    In the second scan the isosurface vertices are created. For this we look at the binary values in a 2x2 neighborhood around each pixel corner. An isosurface vertex must be created if not all four neighboring pixels have the same binary value. Image boundary vertices require special treatment, with pixels falling outside of the image boundary being assigned a predetermined binary value. An additional data structure such as an array is needed to store the association between pixel corners and isocurve vertex indices. The vertex index -1 is used to indicate that a particular vertex corner does not have an associated vertex index.

    In the third scan the vertical edges are generated. Here we need to look at pairs of pixels consecutive in the horizontal direction. An edge has to be created if the two pixels have different binary values. There are two possible cases corresponding to the two possible orientations for the edge. Make sure that you create edges with consistent orientations. To create an edge we need to retrieve the two isocurve vertex indices from the data structure created to store them in the previous step.

    In the fourth scan the horizontal edges are generated. This process is similar to the creation of vertical edges.

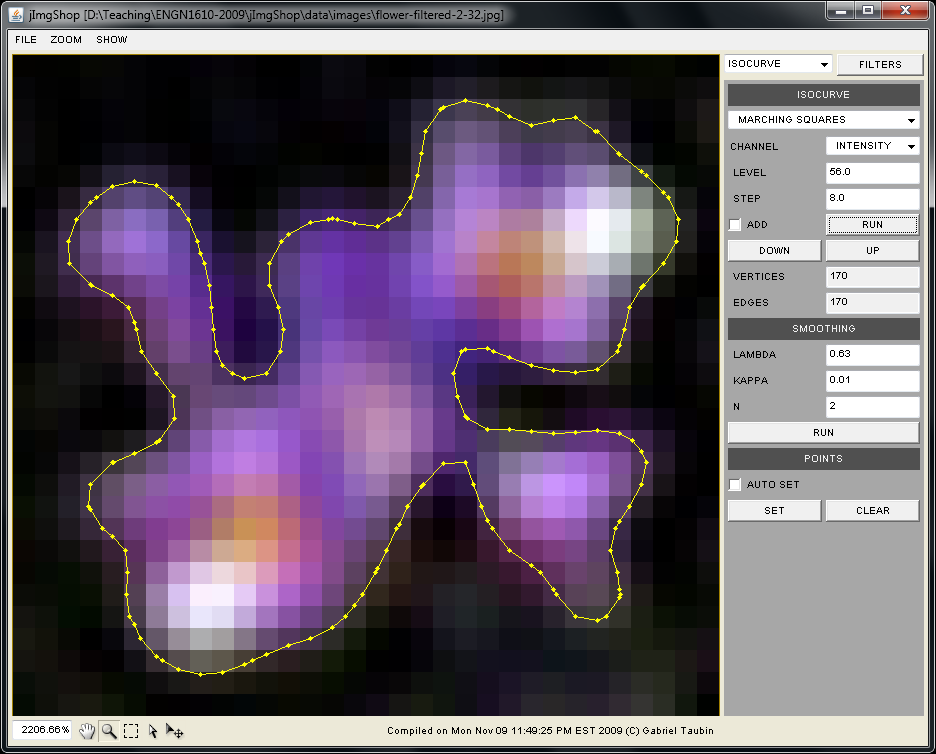
  • public void computeMarchingSquares(float level)



    Read Monday, November 9, and Wednesday, November 11, 2009, class notes.


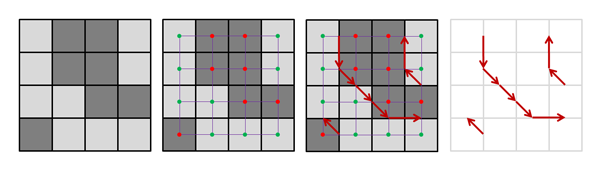
    public void computeRegularTriangulation(float level)



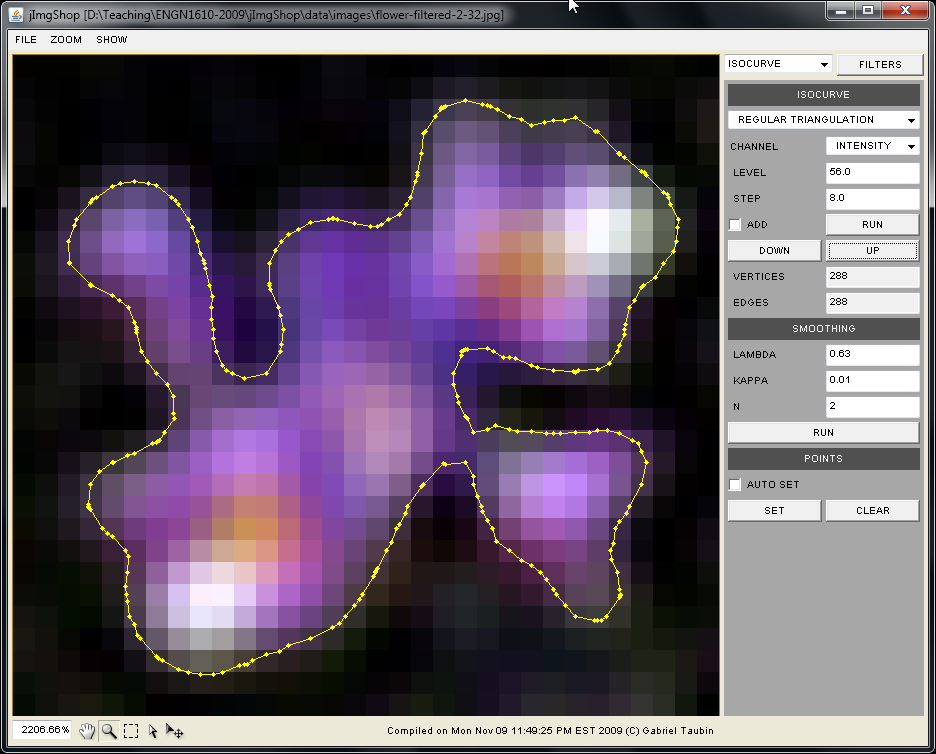
    Read Monday, November 9, and Wednesday, November 11, 2009, class notes.

    public void laplacianSmooth(float lambda0, float lambda1, int nSmooth)

    Read Monday, November 9, and Wednesday, November 11, 2009, class notes, as well as Wednesday, November 11, 2009, smoothing slides.