Embedded Phase Shifting:
Robust Phase Shifting With Embedded Signals
by Baniel Moreno, Kilho Son, and Gabriel TaubinProceeding of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2015
pp. 2301-2309
doi: 10.1109/CVPR.2015.7298843
Dowload the PAPER from this web site. Download the PAPER from the CVF Open Access repository. Dowload the POSTER from this web site.
This project was sponsored by the National Science Foundation.
Brief Description
Embedded Phase Shifting (Embedded PS) is a structured light phase shifting method for 3D scanning presented in CVPR 2015 at Boston. Embedded PS was created at LEMS in Brown University by Daniel Moreno, Kilho Son, and Gabriel Taubin. The main contributions of this paper are:- Projection patterns contain only high spatial frequency sinusoidals, which makes the method robust to global illumination effects and defocus of the illumination source.
- Embedded low frequency phases, not present in the projection patterns, are synthezised during decoding and used for accurate and fast unwrapping of the high frequency phases.
- Multiple measurements, one from each projected high frequency, allow to create more accurate and less noisy 3D models.
- A set of mathematical relations applicable to any periodic signal group is presented which may allow to create `embedded' versions of other SL methods.
@InProceedings{Moreno_2015_CVPR,
author = {Moreno, Daniel and Son, Kilho and Taubin, Gabriel},
title = {Embedded Phase Shifting: Robust Phase Shifting With Embedded Signals},
booktitle = {The IEEE Conference on Computer Vision and Pattern Recognition (CVPR)},
month = {June},
year = {2015}
}
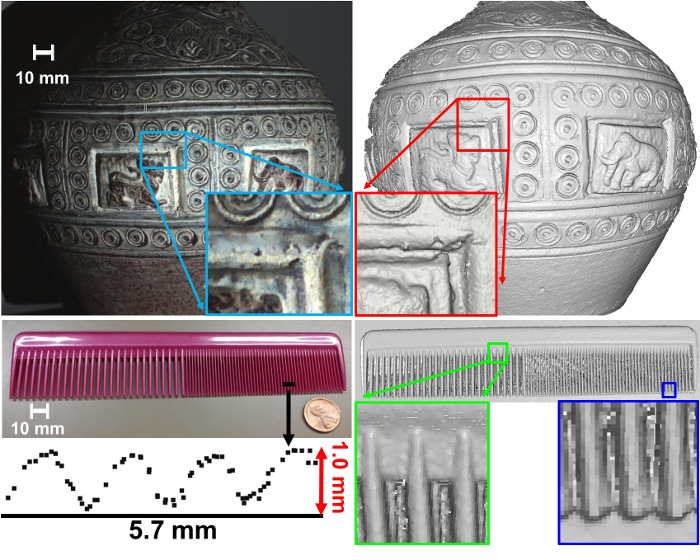
Summary
Objective
To create a Phase Shifting (PS) method for 3D scanning robust to global illumination effects and with low decoding computational cost.
Related work
- Multiple PS
[1] projects patterns of
multiple frequencies and uses Temporal Phase
Unwrapping [2], which is
accurate and computationally efficient, but it
is not robust to global illumination effects.
Frequencies from low to high are projected.
- Micro
PS
[3] is robust to global
illumination effects, because it uses only high
frequency patterns, but decoding requires search in a LUT which is
inefficient and produces frequent errors.
High frequencies only are projected.
Embedded PS
- High frequency patterns robust to global illumination
- Embedded low frequencies permit efficient and accurate phase unwrapping
- Every
projected frequency generates a depth measurement, multiple
measurements combined produce more accurate results.
Only high frequencies are projected, but low frequencies are recovered during decoding.
Coding method
Let be \(\{T_1,\ldots, T_M\}\) real numbers greater than 1. We define \(M\) embedded frequencies \(F_m\) as:
\(F_m = \frac{1}{T_1}\cdots\frac{1}{T_m}.\)
We
define \(M\) pattern
frequencies \(f_m\) as:
\(\begin{bmatrix} f_1\\ f_2\\ f_3\\ \vdots\\ f_M \end{bmatrix} = \begin{bmatrix} 1 &0 &0 & &0\\ 1 &1 &0 & \ldots &0\\ 1 &0 &1 & &0\\ & \vdots& &\ddots&0 \\ 1 & 0&0&\ldots &1 \end{bmatrix} \begin{bmatrix} F_1\\ F_2\\ F_3\\ \vdots\\ F_M \end{bmatrix}. \)
Create a sinusoidal pattern for each of the \(M\) pattern frequencies and project 2 or 3 shifts of each frequency.
Example:
if
\(T_1=16\), \(T_2=8\), and \(T_3=8\); then
- embedded frequencies are \(F_1=1/16\), \(F_2=1/128\), and \(F3=1/1024\)
- pattern frequencies are \(f_1=1/16\), \(f_2=1/14.22\), and \(f_3=1/15.75\)
Decoding method
Use image intensities to recover the phase vector:
\(\mathbf{u}=[o,c_1,s_1,\ldots,c_M,s_M]^T,\ \ c_m=a_m\cos(\omega_m\phi_m),\ s_m=a_m\sin(\omega_m\phi_m).\)
From the phase vector recover pattern frequency phases:
\( \phi_m= \tan^{-1}\dfrac{s_m}{c_m} \)
Extract the embedded frequencies:
\(\left\{\begin{array}{l}
\Phi_1
\equiv \phi_1\\
\Phi_m=\phi_m-\phi_1 \ \ \ \text{for}\
m>1.
\end{array}\right.\)
Use Temporal Phase Unwrapping [2] to unwrap the embedded frequency phases \(\Phi_m\) and pattern frequency phases \(\phi_m\). Each pattern frequency phase provides a separate depth measurement.
Comparison
of PS unwrapping methods
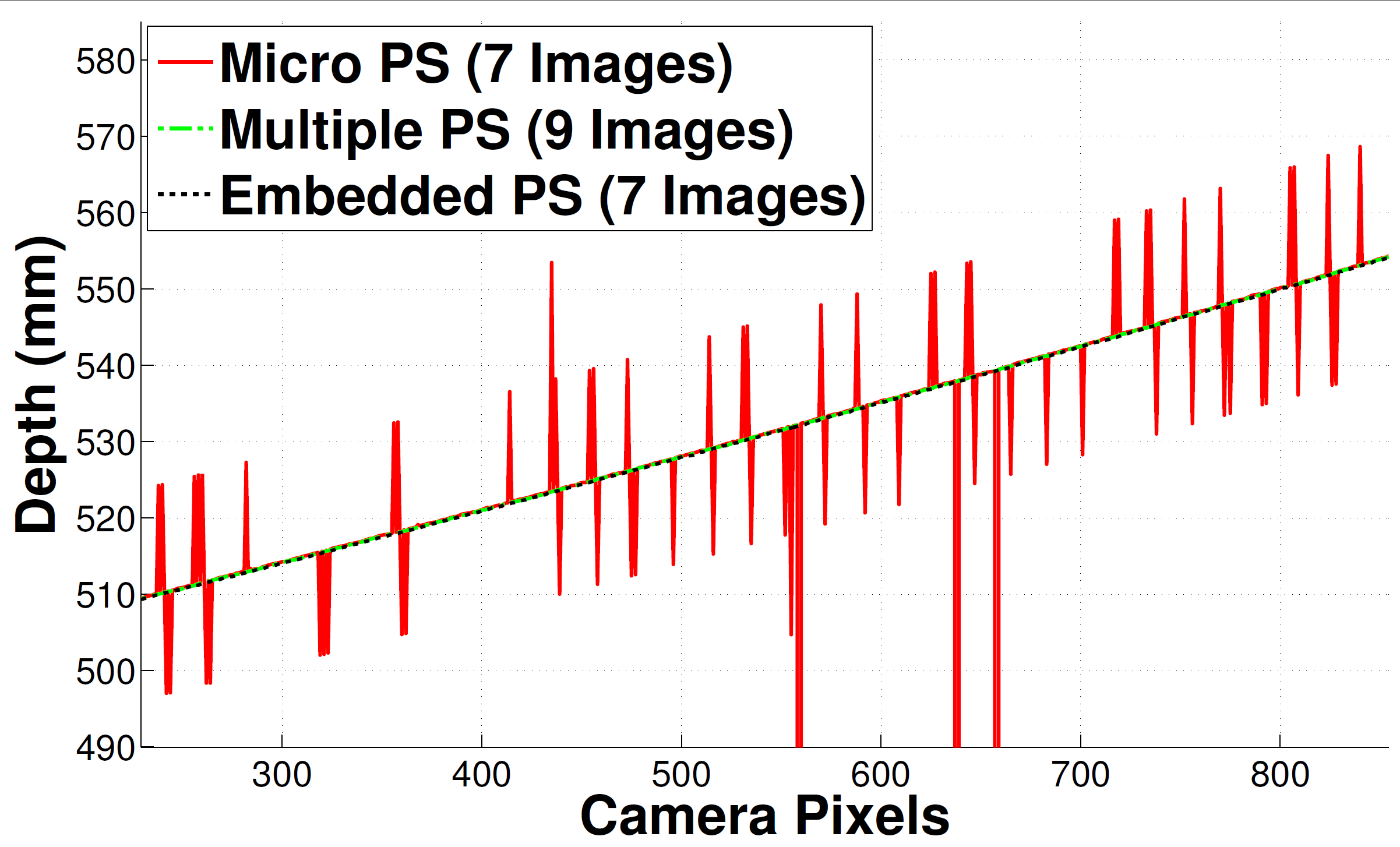
Profile of a metal plane
- Micro PS produces frequent unwrapping errors, some of them can be corrected with a median filter.
- Multiple PS and Embedded PS show now errors.
Surface
Properties
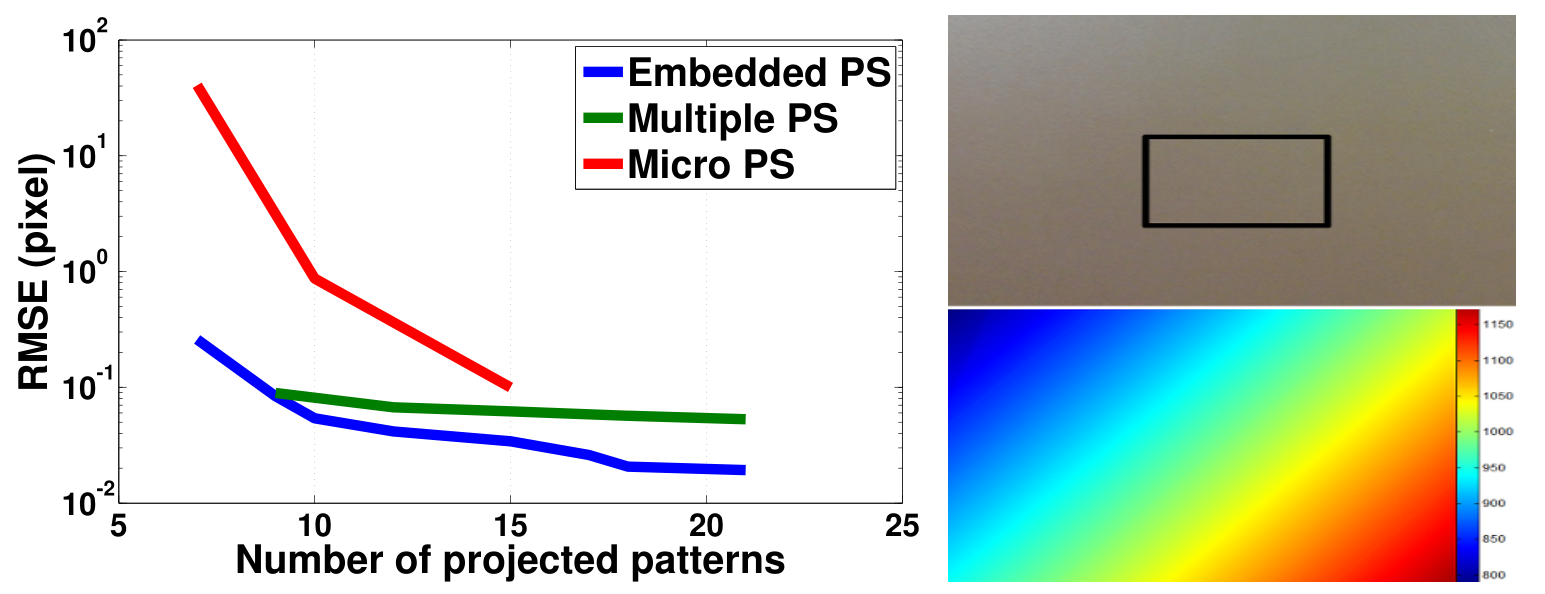
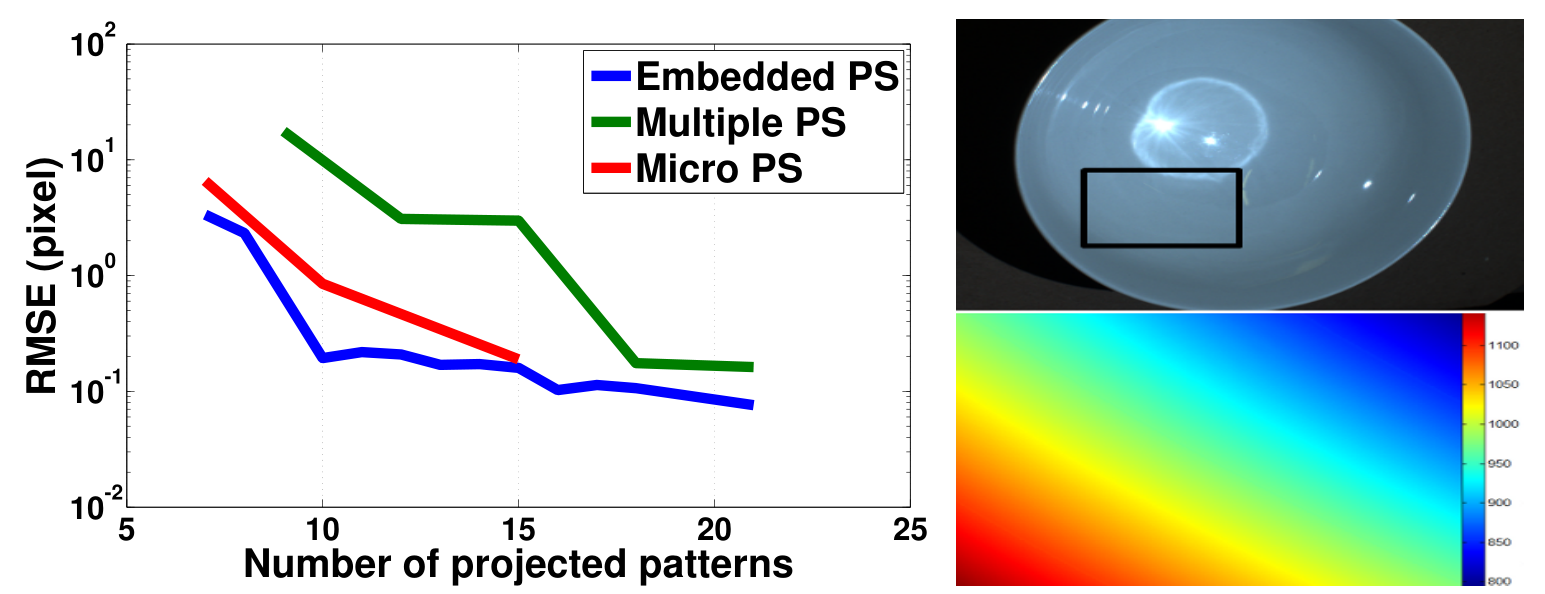
(LEFT) Lambertian surface. (RIGHT) Specular concave surface.
- Lambertian Surface: in the absence of global illumination effects Embedded PS and Multiple PS performs similarly.
- Specular Concave Surface: Embedded PS and Micro PS performs well in the presence of global illumination effects.
Multiple
Measurements
3D models from same image data using only a single measurement (blue) and multiple measurements (red). The latter one has less noise and it is more accurate.
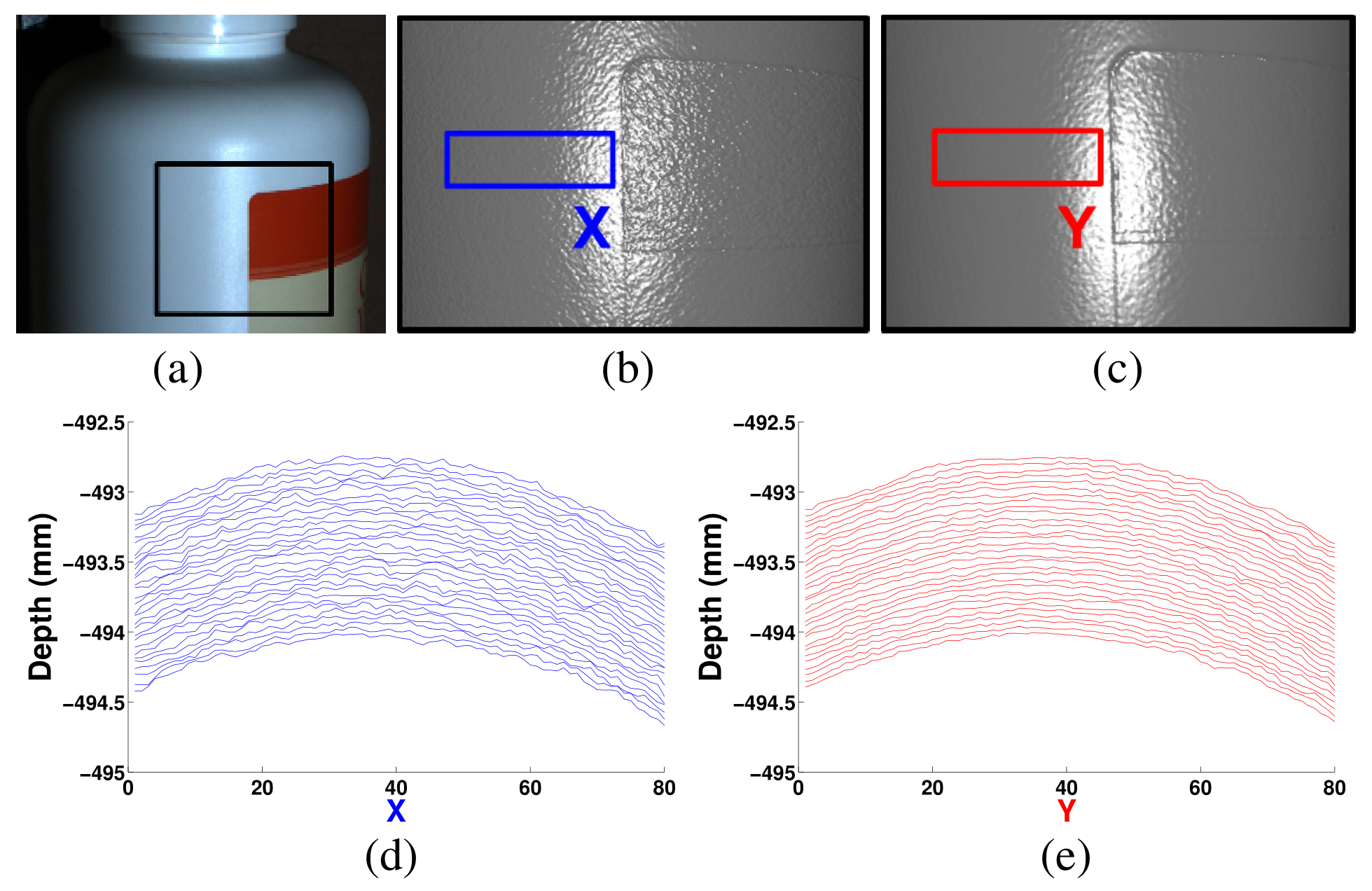
Single vs. Multiple measurements.
3D
Models Comparison
Figure columns: Scene picture, Embedded PS, Micro PS, and Multiple PS
Rectangular Bowl: concave object with specular surface, exhibit strong interreflections.
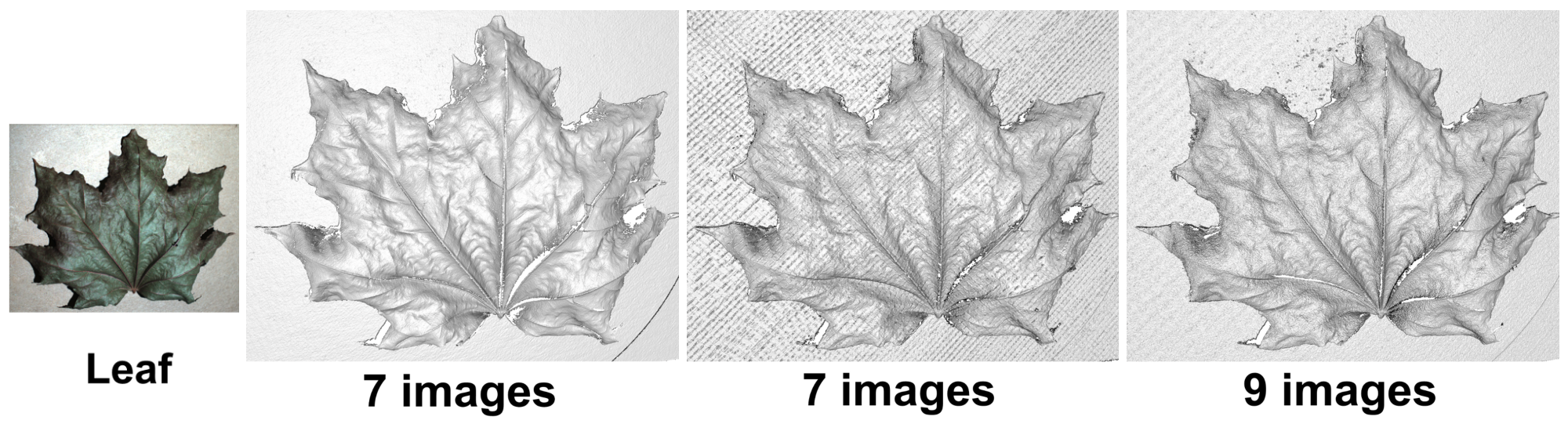
Tree Leaf: fine structures with small details.
Orange: semi translucent skin results in subsurface scattering.
Spatula: polished metal anisotropic surface.
Computation
Complexity
Embedded PS has low coputational complexity, similar to Multiple PS, contrary to Micro PS which executes a search for each image pixel to decode.
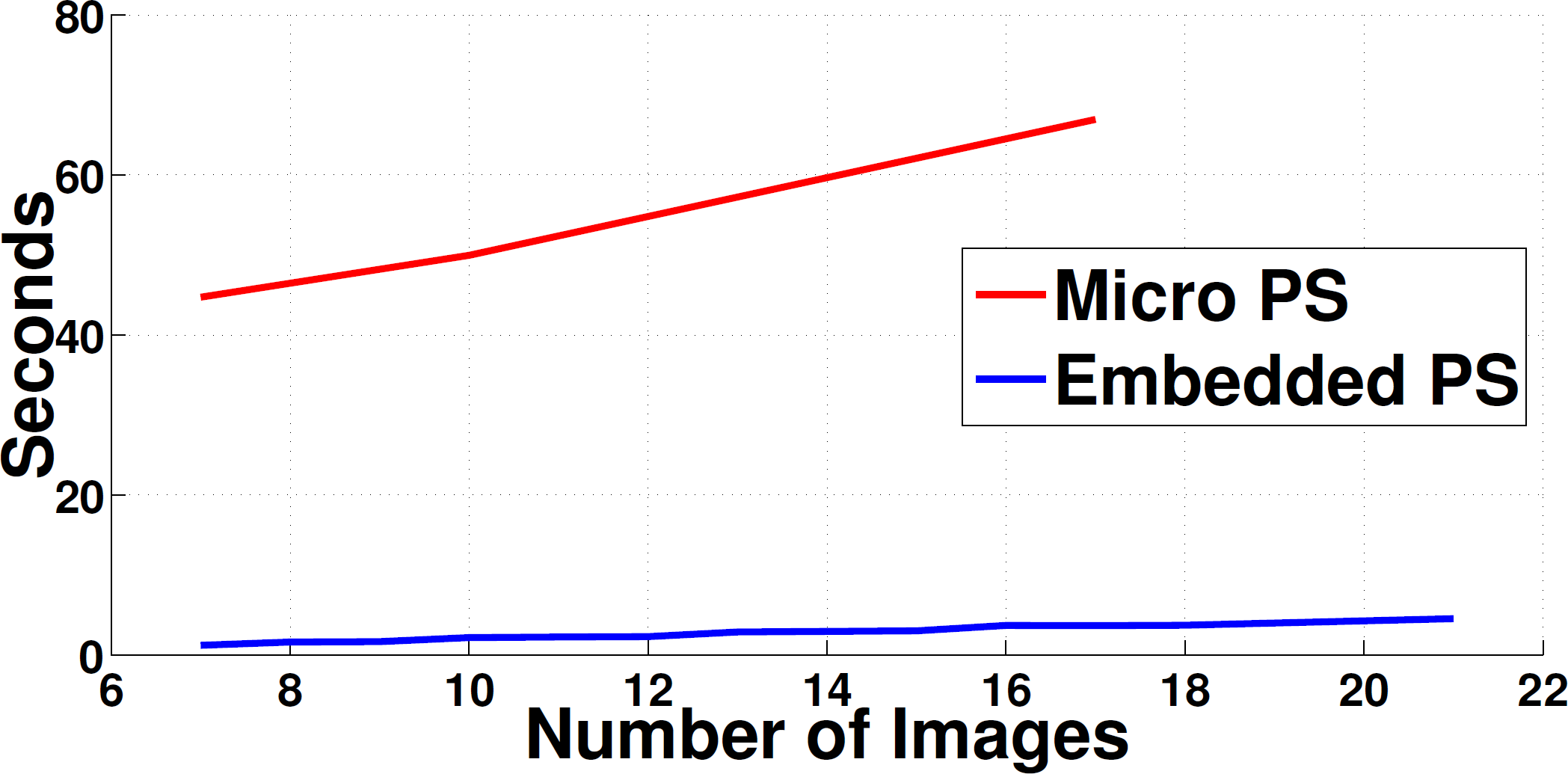
Plot of the decoding algorithm computation time vs. the number of captured images.
Conclusion
Embedded PS is robust to global illumination effects, it is fast and accurate, and produces multiple measurements which are used to generate 3D models with very low noise.
References
- T. Pribanić, H. Dźapo, and J. Salvi. Efficient and low-cost 3D structured light system based on a modified number-theoretic approach. EURASIP, pages 1–11, 2010.
- H. O. Saldner and J. M. Huntley. Temporal phase unwrapping: application to surface profiling of discontinuous objects. Applied optics, 36(13):2770–2775, 1997.
- M. Gupta and S. Nayar. Micro Phase Shifting. In CVPR, pages 1–8, Jun 2012.