Introduction to Geometry Processing Through Optimization
by Gabriel TaubinIEEE Computer Graphics and Applications Volume 32, Issue 4, pages 88 - 94, July-August 2012
Computer representations of piece-wise smooth surfaces have become vital technologies in areas ranging from interactive games and feature film production to aircraft design and medical diagnosis. One of the dominant surface representations is polygon meshes. Simple and efficient geometry processing algorithms to operate on the very large polygon meshes used today are required in most computer graphics applications. In general, developing these algorithms involves fundamental concepts from pure mathematics, algorithms and data structures, numerical methods, and software engineering. As an introduction to the field, in this article we show how to formulate a number of geometry processing operations as the solution of systems of equations in the ``least squares sense.'' The equations are derived from local geometric relations using elementary concepts from analytic geometry, such as points, lines, planes, vectors, and polygons. Simple and useful tools for interactive polygon mesh editing result from the most basic descent strategies to solve these optimization problems. We develop the mathematical formulations incrementally, keeping in mind that the objective is to implement simple software for interactive editing applications that works well in practice. Higher performance versions of these algorithms can be implemented by replacing the simple solvers proposed here by more advanced ones.
Representing Polygon Meshes
There are many ways of representing polygon meshes. Here we adopt an array-based ``Indexed Face Set'' representation, where a polygon mesh \(P=(V,X,F)\) is composed of: a finite set \(V\) of vertex indices, a table of three dimensional vertex coordinates \(X=\left\{x_i:i\in V\right\}\) indexed by vertex index, and a set \(F\) of polygon faces, where a face \(f=\left(i_1,\dots ,i_{n_f}\right)\) is a sequence of vertex indices without repetition. The number \(n_f\) of vertex indices in a face may vary from face to face, and of course every face must have a minimum of \(n_f\ge 3\) vertices. Two cyclical permutations of the same sequence of vertex indices are regarded as the same face, such as \((0,1,2)\) and \((1,2,0)\), but when a sequence of vertex indices results from another one by inverting the order, such as \((0,1,2)\) and \((2,1,0)\), we regard the two sequences as different faces, and say that the two faces have opposite orientations. This representation does not support faces with holes, which is perfectly acceptable for most applications. For each face \(f=\left(i_1,\dots ,i_{n_f}\right)\), \(V\left(f\right)=\{i_1,\dots ,i_{n_f}\}\) is the set of vertex indices of the face considered as a set.
In terms of data structures, if \(N_V\) is the total number of vertices of the mesh, we will always assume that the set of vertex indices is \(\{0,\dots ,N_V-1\}\), composed of consecutive integers starting at \(0\). The vertex coordinates are represented as a linear array of \(3N_V\) floating point numbers, and the set of faces \(F\) is represented as a linear array of integers resulting from concatenating the faces. To be able to handle polygon meshes with faces of different sizes (i.e., different number of vertex indices per face) we also append a special marker at the end of each face, such as the integer -1 which is never used as a vertex index, to indicate the end of the face. For example, \([0,1,2,-1,0,2,3,-1]\) would be the representation for the set of faces \(F\) of a polygon mesh composed of two triangular faces, \(f_0=(0,1,2)\) and \(f_1=(0,2,3)\), and four vertices \(V=\{0,1,2,3\}\) . The particular order of the faces within the linear array is not important, but once a particular order is chosen we will assume that it does not change. We refer to the relative location of a face within the array as its face index. If \(N_F\) is the total number of faces, then the set of face indices is \(\{0,\dots ,N_F-1\}\) .
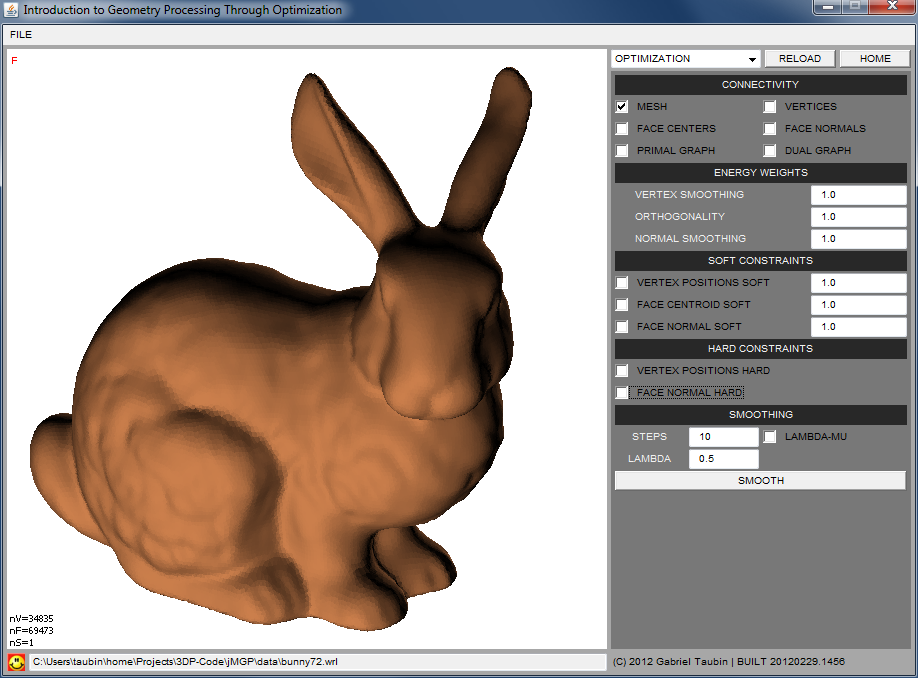
Polygon Mesh Smoothing
Large polygon meshes are usually generated by measurement processes, such as laser scanning or structured lighting, which result into measurement errors or noise in the vertex coordinates. In some cases systematic errors are generated by algorithms which generate polygon meshes, such as isosurface algorithms. In general the noise must be removed to reveal the hidden signal, but without distorting it. Algorithms which attempt to solve this problem are referred to as smoothing or denoising algorithms. It is probably fair to say that the whole field of Digital Geometry Processing grew out of early solutions to this problem. Our goal in this article is to develop a simple and intuitive methodology to attack this problem in various ways. Similar approaches can be used later to formulate other more complex problems, such as large scale deformations for interactive shape design. In these smoothing algorithms removing noise is constrained to changes to the values of the vertex coordinates \(X\). Neither the set of vertex indices \(V\) nor the faces \(F\) of the polygon mesh are allowed to change.
Perhaps the simplest an oldest method to remove noise from a polygon mesh is Laplacian smoothing. In classical signal processing noise is removed from signals sampled over regular grids by convolution, i.e., by averaging neighboring values. Laplacian smoothing is based on the same idea: each vertex coordinate \(x_i\) is replaced by a weighted average of itself and its first order neighbors. But to properly describe this method we first need to formalize a few things.
The Primal Graph of a Polygon Mesh
The graph, or more precisely the primal graph (we will introduce the dual graph later), \(G=(V,E)\) of a polygon mesh \(P=\left(V,X,F\right)\) is composed of the set of polygon mesh vertex indices \(V\) as the graph vertices, and the set \(E\) of mesh edges as the graph edges. A mesh edge is an unordered pair of vertex indices \(e=\left(i,j\right)=\left(j,i\right)\) which appear consecutive to each other, irrespective of the order, in one or more faces of the polygon mesh. In that case we say that the face and the edge are incident to each other. The set of edges incident to a face \(f\) is \(E\left(f\right)\), and \(n_f\) is also the number of edges in this set (equal to the number of vertices in the face); for example, for the face \(f=(0,1,2)\) it is \(E(f)=\{\left(0,1\right),\left(1,2\right),\left(2,0\right)\}\). Note that one or more faces may be incident to a common edge. The set of faces incident to a given edge \(e=(i,j)\) is \(F\left(e\right)\), which has \(n_e\) number of incident faces. A boundary edge has exactly one incident face, a regular edge has exactly two incident faces, and a singular edge has three or more incident edges. We say that two vertices \(i\) and \(j\) are first order neighbors if the pair \((i,j)\) of vertex indices is an edge. For each vertex index \(i\), the set \(V(i)=\{j:(i,j)\in E\}\) is the set of first order neighbors of \(i\), and \(n_i\) is the number of elements in this set.
In terms of data structures, the mesh edges
\(\left(i,j\right)\)can be represented as a linear array of \({2N}_E\)
vertex indices, where \(N_E\) is the total number of polygon mesh
edges. To make the representation of each edge unique, in this array
we store either the pair \(\left(i,j\right)\) if \(i To efficiently construct the array of edges from the array
of faces we use an additional data structure to represent a graph over
the set of vertex indices. This graph data structure is initialized
with the set of vertex indices, and an empty set of edges. The graph
data structure supports two efficient operations:
\(get\left(i,j\right)\) and \(insert(i,j).\) The operation \(get(i,j)\)
returns the edge index assigned to the edge \(\left(i,j\right),\) if
such edge exists, and a unique identifier such as -1 which is not used
as an edge index, if the edge \(\left(i,j\right)\) does not yet belong
to the set of edges. If the edge \((i,j)\) does not yet exists, the
operation \(insert(i,j)\) appends the pair of indices to the array of
edges and assigns its location in the array to the edge as the unique
edge index. In this way, the index \(0\) is assigned to the first edge
created, and consecutive indices are assigned to edges created
afterwards. An efficient implementation of this graph data structure
can be based on a hash table.
For some algorithms it is useful to have efficient method to
determine the number \(n_e\)of incident faces per edge, as well as to
access the indices of those faces. The graph data structure can be
extended to support this functionality. The number \(n_e\)can be
represented as an additional field in the record used to represent the
edge \(e\) in the graph data structure, or as an external variable
length integer array. Each value is initialized to 1 by the
\(insert(i,j)\) operation, during the construction of the graph data
structure, and incremented during the traversal of the array of faces,
every time the \(get\left(i,j\right)\) operation returns a valid face
index. The sets of faces \(F(e)\) incident to the edges can be
represented as an array of variable length arrays indexed by edge
index, and can be constructed as well during the construction of the
graph data structure.
A large family of polygon mesh editing algorithms comprise
three steps: 1) for each vertex index \(i\) of the polygon mesh, compute
a vertex displacement vector \(\triangle x_i\) (in general as a function
of the original vertex coordinates \(X\), as well as of some external
constraints or user input); 2) after all the vertex displacement
vectors are computed, apply the vertex displacement vectors to the
vertex coordinates \(x'_i=x_i+\lambda \triangle x_i\) ,where \(\lambda
\) is a fixed scale parameter (either user-defined or also computed
from the polygon mesh data); and 3) replace the original vertex
coordinates \(X\) by the new vertex coordinates \(X'\). The three steps
are repeated for a certain number of times specified in advance by the
user, or until a certain stopping criterion is met.
All the algorithms discussed in this article are members of
this family. In terms of storage, these algorithms require an
additional linear array of \(3N_V\) floating point numbers to represent
the vertex displacement. The vertex coordinates are updated using this
procedure in linear time as a function of the number of vertices. Of
course, the time and storage complexity of evaluating the vertex
displacements, to determine the scale parameter, and to determine
whether the stopping criterion is met when a stopping criterion is
used, have to be added to the overall complexity of the algorithm. In
general, algorithms with overall linear time and storage complexity as
a function of the polygon mesh size are the only algorithms which
scale properly to be of practical use with very large polygon meshes.
As mentioned above, in Laplacian smoothing each vertex coordinate
\(x_i\) is replaced by a weighted average of itself and its first order
neighbors. More precisely, for each vertex index \(i\), a vertex
displacement vector\textbf{}
\[
\triangle x_i=\frac{1}{n_i}\sum_{j\in
V(i)}{(x_j-x_i)}
\]
is computed as the average over the first order
neighbors \(j\) of vertex \(i\), of the vectors \(x_j-x_i\). After all these
displacement vectors are computed as functions of the original vertex
coordinates \(X\), we apply the vertex displacement to the vertex
coordinates with a scale parameter in the range \(0<\lambda
<1\) (\(\lambda =1/2\) is usually a good choice).
To compute vertex displacement vectors, it looks as though
an efficient way of finding all the first order neighbors of each
vertex index is needed, and in particular the number of elements in
the sets of first order neighbors. Unfortunately the data structures
introduced so far do not provide such methods. However, since each
edge \(\left(i,j\right)\) contributes a term to the sums defining both
displacement vectors \(\triangle x_i\)and \(\triangle x_j\), all the
displacement vectors can be accumulated together while linearly
traversing the array of edges. During the same traversal we also have
to accumulate the number of first order neighbors of each vertex, so
that the vertex displacement vectors can be normalized. In summary,
the algorithm comprises the following steps: 1) for every vertex index
\(i\), set \(\triangle x_i=0\) and \(n_i=0\); 2) for each edge \((i,j)\), add
\(x_i-x_j\) to \(\triangle x_j\), add \(x_j-x_i\) to \(\triangle x_i\), and
increment \(n_i\) and \(n_j\) by 1; and 3) for each vertex index \(i\) so
that \(n_i\ne 0\), divide \(\triangle x_i\) by \(n_i\).
Let us consider the sum of the squares of the edge lengths
\(\left\|x_i-x_j\right\|\) as a function of the vertex coordinates of a
polygon mesh
\[
E(x)=\sum_{(i,j)\in E}{{\left\|x_j-x_i\right\|}^2}
\]
where \(x\) is the table of vertex coordinates \(X\) regarded as a column
vector of dimension \(3N_V\), resulting from concatenating all the \(N_V\)
three dimensional vertex coordinates \(x_i\). Note that as a function of
\(x\), this function is quadratic, homogeneous, and non-negative
definite. As a result, it attains the global minimum \(0\) when all the
edges have zero length, or equivalently, when all the vertex
coordinates have the same value. As a result, starting from noisy
vertex coordinates \(X\), computing the global minimum of this function
does not constitute a smoothing algorithm, but taking a small step
along a descent direction towards a local minimum (which in this case
is the global minimum), is still a valid heuristic. Gradient descent
is the simplest iterative algorithm to locally minimize a function
such as this one. The negative of the gradient of the function \(E(x)\)
is the direction of steepest descent. We can look at the gradient of
\(E(x)\) as the concatenation of the \(N_V\)three dimensional
derivatives of \(E(x)\) with respect to the vertex coordinates \(x_i\)
\[
\frac{\partial E}{\partial x_i}=\sum_{j\in
V(i)}{(x_i-x_j)}=-\sum_{j\in V(i)}{(x_j-x_i)}
\]
To construct a descent algorithm, we still need to choose a positive
scale parameter \(\lambda \) so that the vertex coordinates update
rule\(x'_i=x_i-\lambda \frac{\partial E}{\partial x_i}\)actually
results in the value of the function to decrease: \(E(x') Although we can already observe a close connection between
this method and Laplacian smoothing, the descent directions chosen in
both cases are not identical. Why is that so?
The Jacobi iteration is the simplest iterative method to
solve large square diagonally dominant systems of linear equations
\(Ax=b\), where the \(i\)-th. equation is solved independently for the
\(i\)-th. variable, keeping the other variables fixed, resulting in a
new value for the \(i\)-th. variable. After the new values for all the
variables are determined in this way, the old variables are replaced
by, or displaced in the direction of, the new variables, and the
process is repeated for a fixed number of iterations, or until
convergence. Under certain conditions the method converges to the
solution of the system of equations. In the context of optimizing a
quadratic function \(E(x)\), the system of equations to be solved
corresponds to making the gradient of the function equal to zero. Even
when the performance function is not a quadratic function of the
variables, this method can be used to construct a properly scaled
descent algorithm. This ``generalized'' Jacobi iteration is equivalent
to minimizing the function \(E(x)\) with respect to the \(i\)-th. variable
independently. If we write the new value for the variable \(x_i\) as the
old value plus a displacement \(x_i+\triangle x_i\), in the case of the
sum of square edge lengths function, determining the displacement
\(\triangle x_i\) reduces to solving the equation
\[
0=\frac{\partial E}{\partial x_i}\left(x_1,\dots ,x_i+\triangle
x_i,\dots ,x_{N_V}\right)=\sum_{j\in V(i)}{\left(\triangle
x_i+x_i-x_j\right)}=n_i\triangle x_i-\sum_{j\in V(i)}{(x_j-x_i)}
\]
which results in the Laplacian smoothing displacement vector. The
optimal value for the parameter \(\lambda \) can be determined by
minimizing \(E(x+\lambda \Delta x)\) with respect to \(\lambda \) as
described above, although \(\lambda =1/2\) usually works well in
practice.
Laplacian smoothing is a very simple algorithm, and it is
quite easy to implement. It does produce smoothing, but when too many
iterations are applied, the shape of the polygon mesh undergoes
significant and undesirable deformations. As mentioned above, this is
due to the fact that the function \(E{\rm (}x{\rm )}\) being minimized
has a global minimum (actually infinitely many, but unique modulo a
three dimensional translation) which does not correspond to the result
of removing noise from the original vertex coordinates. Any
converging descent algorithm will approach that minimum, which is why
we observe significant deformations in practice. In our case, in
Laplacian smoothing all the vertex coordinates of the polygon mesh
converge to their centroid
\[
\frac{1}{N_V}\sum^{N_V}_{i=1}{x_i}
\]
In the literature this problem is referred to as ``shrinkage''. Many
algorithms, based on different mathematical formulations ranging from
signal processing to partial differential equations, have been
proposed over the last fifteen or more years to deal with, and solve,
the shrinkage problem. But we are not going to survey these algorithms
here. For the sake of simplicity we take the point of view that the
shrinkage problem is a direct result of the ``wrong'' performance
function being minimized. As a result, we address the shrinkage
problem by modifying the performance function being
minimized. However, after constructing each new performance function,
we follow the same simple steps described above of minimizing the
function with respect to each variable independently to obtain a
properly scaled descent vector, and then updating the variables as in
Laplacian smoothing by displacing the vertex coordinates in the
direction of this descent vector. Finally, we repeat the process for
a predetermined number of steps, or until convergence based on an
error tolerance stop.
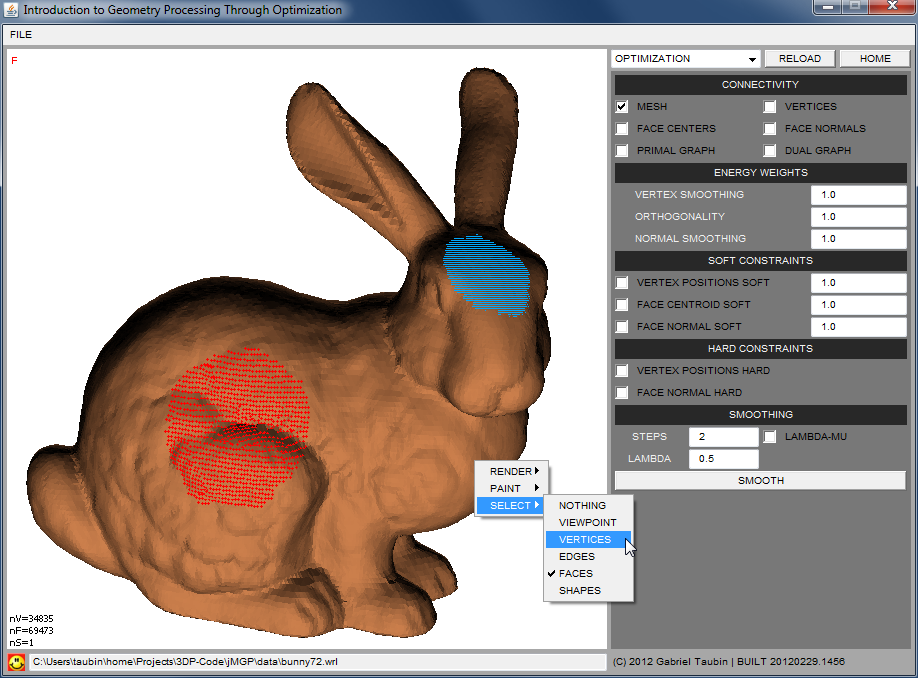
The most obvious way to prevent shrinkage is not to update
all the vertex coordinates. More formally, we partition the set of
vertex indices \(V\) into two disjoint sets, a set \(V_C\) of constrained
vertex indices, and a set \(V_U\) of unconstrained vertex indices. We
also partition the vector of vertex coordinates \(x\) into a vector of
constrained vertex coordinates \(x_C\) and a vector of unconstrained
vertex coordinates \(x_U\). We keep the same sum of squares of edge
lengths function\(E\left(x\right)=E(x_U,x_V)\), but we regard it as a
function of only the unconstrained vertex coordinates \(x_U\), and the
constrained vertex coordinates \(x_V\) are regarded as constants. As
such this function is still quadratic and non-negative definite, but
it is no longer homogeneous. In general, this function still has a
unique minimum (modulo a translation in this case) which has a closed
form expression, and the minimum does not correspond to placing all
the vertices at a single point in space. If we apply the same approach
described above to compute a descent direction by minimizing
\(E\left(x_U\right)\) with respect to each unconstrained variable
independently, we end up with the same descent vectors as in Laplacian
smoothing, and the same descent algorithm, but here only the
unconstrained vertex coordinates are updated. So, the computational
cost of this algorithm is about the same as Laplacian smoothing.
Unfortunately we still observe ``shrinkage''. In general it
is not clear what vertices should be constrained and which ones should
be free to move, but within an interactive modeling system which
allows for interactive selection of vertices this is an effective way
of smoothing out selected portions of a polygon mesh, which we have
found to be useful in practice.
Rather than keeping the constrained vertices at their
original positions, they can be assigned new ``target'' positions, in
which case the constrained vertices can be updated first, and then
kept fixed during the iterations of the algorithm. Unfortunately, if
the constrained vertex displacements are large compared with the
average length of edges, this algorithm may result into noticeable
shape artifacts during the iterations. An alternative is to switch
from this ``hard'' constraints strategy to a ``soft'' constraints
strategy. In a ``soft'' constraints strategy all the variables are
free to move again, and the constraints are satisfied in the ``least
squares'' sense by adding one or more additional terms to the function
being minimized. For example, in our case we consider this function
\[
E\left(x\right)=\sum_{\left(i,j\right)\in
E}{{\left\|x_j-x_i\right\|}^2}+\mu \sum_{i\in
V_C}{{\left\|x_i-x^0_i\right\|}^2}
\]
where \(\mu \) is a positive constant, the second sum is over the
constrained vertices, and \(x^0_i\) is a target constrained vertex
position provided as input data to the algorithm. By applying the
strategy of minimizing each variable independently, we obtain the same
expression as in Laplacian smoothing for the displacements \(\triangle
x_i\) corresponding to the unconstrained vertices, and
\[
\triangle x_i=\frac{1}{n_i+\mu }\left(\sum_{j\in
V(i)}{\left(x_j-x_i\right)+\mu (x^0_i-x_i)}\right)
\]
for the displacements corresponding to the constrained vertices.
It turns out that to produce acceptable results with the
vertex position constraints strategy a large proportion of the
vertices must be constrained, and in that case it is not clear in
general where the target constrained vertex positions should be
placed. Rather than imposing constraints on vertex positions, we
impose similar constraints on some or all of the face centroids. The
intuition here is that the face centroids being weighted averages of
the face vertex coordinates, can be regarded as the result of a
smoothing process, and the problem is how to transfer that smooth
shape information back from the face centroids to the vertex
coordinates. Continuing with the soft constraints approaches, we
consider the following performance function, which looks very similar
to the one used to impose soft vertex constraints
\[
E\left(x\right)=\sum_{\left(i,j\right)\in
E}{{\left\|x_j-x_i\right\|}^2}+\mu \sum_{f\in
F_C}{{\left\|x_f-x^0_f\right\|}^2}
\]
where \(F_C\) is the subset of constrained faces (it could be all the
faces), and for each face \(f=\left(i_1,\dots ,i_{n_f}\right)\), we
express the centroid \(x_f\)as the average of the face vertex
coordinates
\[
x_f=\frac{1}{n_f}(x_{i_1}+\dots +x_{i_{n_f}})
\]
so that the overall function can be regarded as a function of only the
vertex coordinates, and \(x^0_f\) is the target three dimensional point
value for the face centroid. For example, \(x^0_f\) could be the initial
value for the face centroid before any smoothing is applied. Even
though we would start the algorithm with the term of the performance
function corresponding to the face centroid constraints identical to
zero, it may become nonzero after one or more iterations while the
overall function decreases. By applying the generalized Jacobi
strategy of minimizing with respect to each variable independently, we
obtain the following expression for each displacement \(\triangle x_i\)
\[
\triangle x_i{\rm =}\frac{1}{n_i+\mu \sum_{f\in
F_C(i)}{\frac{1}{n_f}}}\left(\sum_{j\in V(i)}{(x_j-x_i)}+\mu
\sum_{f\in F_C\left(i\right)}{\frac{1}{n_f}}(x^0_f-x_f)\right)
\]
where \(F_C(i)\) is the subset of constrained faces \(f\) which contain
the vertex index \(i\). These displacements and normalization factors
can be accumulated as in previous algorithms by initializing to zero,
traversing the array of edges, traversing the array of constrained
faces, and then normalizing. Once the displacements are computed, the
vertex coordinates are updated as in Laplacian smoothing.
None of the constraints discussed so far allow for direct
control of local surface orientation. A smoothing algorithm able to
selectively control local surface orientation is a useful tool within
an interactive polygon mesh editing system, and yet another possible
way to prevent the shrinkage problem of Laplacian smoothing. To be
able to control surface orientations, we need to introduce surface
normal vectors into the performance function to be minimized. As we
have done for the face centroids, one possibility is to derive an
expression for a face normal vector as a function of the face vertex
coordinates, and then add an error term to the performance function
for all or some of the faces. Since doing so results in nonlinear
equations to solve for the displacement vectors, we propose a simpler
alternative approach. We consider the following performance function
\[
E\left(x\right)=\sum_{(i,j)\in E}{{\left\|x_j-x_i\right\|}^2}+\mu
\sum_{f\in F_N}{\sum_{(i,j)\in E(f)}{{(u^t_f(x_j-x_i))}^2}}
\]
where the first term is the sum of square edge lengths as in all the
previous performance functions, and the second term is a sum over a
subset \(F_N\) of faces where we want to impose the face normal
constraint, and the edges \(\left(i,j\right)\) incident to each face \(f\)
of this set. For each such face-edge pair we impose as a soft
constraint that the face normal vector \(u_f\) be orthogonal to the face
boundary vector \(x_j-x_i\). The face normal vectors \(u_f\) are provided
by the user as additional inputs to the algorithm. Although in our
polygon mesh representation the faces are not forced to be planar, for
the faces to be planar, this condition must be satisfied for all the
face boundary vectors of each face. Note that with the constrained
face normal vectors regarded as constants, this performance function
is also quadratic and homogeneous in the vertex coordinates. In this
case the displacement vectors satisfy the following linear equations
\[
\left(n_iI+\mu \sum_{f\in F_N(i)}{\sum_{j\in
V(f,i)}{n_fn^t_f}}\right)\triangle x_i=\sum_{j\in
V(i)}{(x_j-x_i)}+\mu \sum_{f\in F_N(i)}{\sum_{j\in
V(f,i)}{n_fn^t_f}}(x_j-x_i)
\]
where \(I\) is the \(3\times 3\) identity matrix,
\(V\left(f,i\right)=V(f)\cap V(i)\) is the set of vertices which belong
to the face \(f\) and are first order neighbors of vertex \(i\) (there are
exactly two such vertices when the face is known to contain vertex
\(i\)). The \(3\times 3\) matrix on the left hand side multiplying
\(\triangle x_i\), which is symmetric and positive definite, and can be
accumulated during the mesh traversal along with the other sums, can
be easily inverted using Cholesky decomposition.
Now let's assume that we have a face normal vector \(u_f\) for
every face of the polygon mesh. We concatenate these face normal
vectors to form a vector \(u\) of dimension \(3N_F\) which we consider not
a constant provided by the user, but as a new variable. The variables
\(u\) and \(x\) are of course not independent, but, rather than imposing
their relations as hard constraints, we regard them as independent
variables, and represent their relations as soft constraints as in the
case of face normal constraints. To remove noise from the face normal
vectors we consider the performance function
\[
E\left(u\right)=\sum_{(f,g)\in E^*}{{\left\|u_f-u_g\right\|}^2}
\]
This is the sum over the dual mesh edges of the square differences of
face normal vectors. The set of dual mesh edges \(E^*\) is composed of
pairs \((f,g)\) of faces which share a regular edge (one which has
exactly two incident faces). Formally, the dual graph of a mesh has
the faces of the mesh as dual graph vertices, and the dual mesh edges
as dual graph edges. It is important to note the similarity between
this performance function on the sum of square edge lengths.
If we initialize the face normal vectors from the vertex
coordinates, this performance function can be used to first remove
noise from the face normal vectors, and then use the smoothed face
normal as face normal constraints in a second smoothing process
applied to the vertex coordinates. This second process of smoothing
the vertex coordinates with face normal constraints can be regarded as
the integration of the smoothed face normals. Applying the generalized
Jacobi strategy to this performance function, we can compute a
displacement vector \(\triangle u_f\) for the face normal vectors. Since
after these face normal displacements are applied, the face normal
vectors may no longer be unit length, we normalize the updated face
normal vectors to unit length, and then perform the face normal
integration step.
Another alternative is to consider the following performance
function
\[
E\left(x,u\right)=\sum_{(i,j)\in E}{{\left\|x_j-x_i\right\|}^2}+\mu
\sum_{f\in F}{\sum_{(i,j)\in E(f)}{{(u^t_f(x_j-x_i))}^2+\gamma
\sum_{(f,g)\in E^*}{{\left\|u_f-u_g\right\|}^2}}}
\]
and apply the Jacobi minimization strategy on the variables \(x\) and
\(u\) together. In this way we can determine displacement vectors
\(\triangle x_i\) and \(\triangle u_f\) as functions of the variables \(x\)
and \(u\), and then update both variables at once, followed by
normalization of face normal vectors to unit length. We leave the
details of these derivations to the reader.
Note that the two approaches discussed here allow for hard
constraints to be applied to a subset of face normal vectors. As in
the case of hard vertex coordinate constraints, the constrained values
are just not updated. Also soft face normal constraints can be imposed
by adding yet another term to the last performance function composed
of the sum over a subset of faces of square errors between face normal
vectors and target face normal vectors.
We have considered a number of ways to add constraints to
Laplacian smoothing. All these strategies can be combined into a
single general polygon mesh smoothing algorithm which allows to impose
hard and soft vertex constraints on disjoint subsets of vertex
indices, soft face centroid constraints on a subset of faces, and hard
and soft face normal constraints on disjoined subset of faces. And all
these constraints can be applied simultaneously.
Following the same strategy constraints on higher order
properties such as curvature can be imposed, but at this point we will
let the reader to figure out how to do so.
Vertex Evolution Algorithms
Laplacian Smoothing
Descent Algorithms
The Jacobi Iteration
How to fix Laplacian Smoothing
Vertex Position Constraints
Face Centroid Constraints
Face Normal Constraints
Smoothing Face Normal Vectors
Combining all the Smoothing Strategies
